
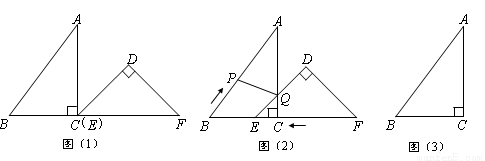
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm。
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动。当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移。DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5)。解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由。
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由。(图(3)供同学们做题使用)
(1)2;(2)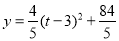 ,当t=3时,y最小=
,当t=3时,y最小=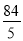 .(3)1s.
.(3)1s.
【解析】
试题分析:(1)因为点A在线段PQ垂直平分线上,所以得到线段相等,可得CE=CQ,用含t的式子表示出这两个线段即可得解;
(2)作PM⊥BC,将四边形的面积表示为S△ABC-S△BPE即可求解;
(3)假设存在符合条件的t值,由相似三角形的性质即可求得.
(1)∵点A在线段PQ的垂直平分线上,
∴AP=AQ.
∵∠DEF=45°,∠ACB=90°,∠DEF+∠ACB+∠EQC=180°,
∴∠EQC=45°.
∴∠DEF=∠EQC.
∴CE=CQ.
由题意知:CE=t,BP=2t,
∴CQ =t.
∴AQ=8-t.
在Rt△ABC中,由勾股定理得:AB=10cm .
则AP=10-2t.
∴10-2t=8-t.
解得:t=2.
答:当t=2s时,点A在线段PQ的垂直平分线上.
(2)过P作PM⊥BE,交BE于M,


∴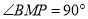 .
.
在Rt△ABC和Rt△BPM中,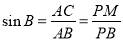 ,
,
∴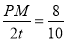 .
.
∴PM=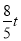 .
.
∵BC=6cm,CE=t,
∴ BE=6-t.
∴y = S△ABC-S△BPE =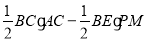
=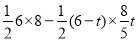
=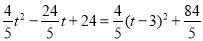 .
.
∵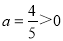 ,
,
∴抛物线开口向上.
∴当t=3时,y最小=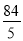 .
.
答:当t=3s时,四边形APEC的面积最小,最小面积为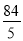 cm2.
cm2.
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上.
过P作PN⊥AC,交AC于N,
∴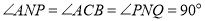 .
.
∵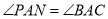 ,
,
∴△PAN ∽△BAC.
∴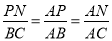 .
.
∴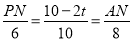 .
.
∴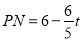 ,
,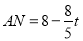 .
.
∵NQ=AQ-AN,
∴NQ=8-t-(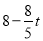 ) =
) =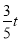 .
.
∵∠ACB=90°,B、C(E)、F在同一条直线上,
∴∠QCF=90°,∠QCF =∠PNQ.
∵∠FQC =∠PQN,
∴△QCF∽△QNP .
∴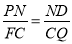 .
.
∴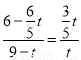 .
.
∵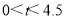
∴
解得:t=1.
答:当t=1s,点P、Q、F三点在同一条直线上.
考点:1.二次函数的最值;2.线段垂直平分线的性质;3.勾股定理;4.相似三角形的判定与性质.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题四数学试卷(解析版) 题型:选择题
在下列图形中,既是轴对称图形又是中心对称图形的是 ( )

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:选择题
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若△CDN的面积与△CMN的面积比为1︰5,则  的值为( ).
的值为( ).

A.2 B.4 C. D.
D.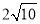
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题三数学试卷(解析版) 题型:填空题
我校为帮扶学校的留守儿童举行了捐款活动,初三(1)班第一小组八名同学捐款数额(元)分别为:20,50,30,10,50,100,30,50.则这组数据的中位数是__________。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级3月月考数学试卷(解析版) 题型:解答题
我市高新技术开发区的某公司,用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价,需定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件新产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利为w(万元).(年获利=年销售额-生产成本-投资成本)
(1)直接写出y与x之间的函数关系式;
(2)求第一年的年获利w与x间的函数关系式,并说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?
(3)若该公司希望到第二年底,除去第一年的最大盈利(或最小亏损)后,两年的总盈利不低于1842元,请你确定此时销售单价的范围.在此情况下,要使产品销售量最大,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级下学期期中考试数学试卷(解析版) 题型:选择题
2014年3月31日凌晨,重庆东水门长江大桥正式通车,重庆主城再添一座跨江大桥,为重庆的经济发展提供了帮助.王大爷为了感受重庆交通的发展,搭乘公交车从家去参观东水门长江大桥,预计1个小时能到达.行驶了半个小时,刚好行驶了一半路程,遇到堵车道路被“堵死”,堵了几分钟突然发现旁边刚好有一个轻轨站,于是王大爷转乘轻轨去观看大桥(轻轨速度大于公交车速度),结果按预计时间到达.下面能反映王大爷距大桥的距离y(千米)与时间x(小时)的函数关系的大致图象是( )




A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com