练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（　　）
    A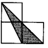．B．C．D．

    分析 利用△ABC中，∠ACB=135°，AC=2，BC=$\sqrt{2}$，然后根据两组对应边的比相等且夹角对应相等的两个三角形相似可对各选项进行判定即可．

    解答 解：在△ABC中，∠ACB=135°，AC=2，BC=$\sqrt{2}$，
    在A、C、D选项中的三角形都没有135°，而在B选项中，三角形的钝角为135°，它的两边分别为1和$\sqrt{2}$，
    因为$\frac{2}{\sqrt{2}}$=$\frac{\sqrt{2}}{1}$，所以B选项中的三角形与△ABC相似．
    故选B．

    点评 此题考查了相似三角形的判定．注意两组对应边的比相等且夹角对应相等的两个三角形相似．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．函数y=$\frac{1}{1-2x}$中自变量的取值范围是x≠$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，将半径为6的圆形纸片，分别沿AB、BC折叠，若弧AB和弧BC折后都经过圆心O，则阴影部分的面积是12π（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．为弘扬中华传统诗词文化，营造书香校园文化氛围，某校初二年级组织了“书香校园之中华好诗词大赛”，琪琪根据比赛中七位评委所给的某位参赛选手的分数，制作了一个表格（见表），如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（　　）
     中位数 众数 平均数 方差
     9.1 9.2 9.1 0.2
    A．中位数B．众数C．平均数D．方差

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列运算正确的是（　　）
    A．a3+a2=2a5B．a6÷a2=a3C．a4•a3=a7D．（ab2）3=a2b5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．-2的绝对值是（　　）
    A．-2B．$\frac{1}{2}$C．±2D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．若等式x2+px+q=（x+1）（x-3）成立，则p+q=-5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．为了调查瑞州市2016年初三年级学生的身高，从中抽取出200名学生进行调查，这个问题中样本容量为（　　）
    A．被抽取的200名学生的身高B．200
    C．200名D．初三年级学生的身高

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，梯形ABCD中，AD∥BC，AD：BC=1：3，对角线AC与BD相交于点O，AE⊥BC，垂足为E，AE恰好过BD的中点F，∠FBE=30°
    （1）求证：△AOF是等边三角形；
    （2）若BF和OF是关于x的方程x2-（k-2）x+k=0的两根，试求k的值，并求梯形ABCD的面积．

    查看答案和解析>>

    同步练习册答案