
����Ŀ����ͼ1����ABC��![]() AC��BC��AC���Ƶ�C˳ʱ����ת�á�DEC������AB������DE�ڵ�F��
AC��BC��AC���Ƶ�C˳ʱ����ת�á�DEC������AB������DE�ڵ�F��
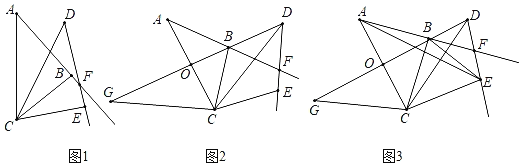
��1����AFD���BCE�Ĺ�ϵ���� ����
��2����ͼ2������ת��Ϊ60��ʱ����D����B���߶�AC���е�Oǡ����ͬһֱ���ϣ��ӳ�DO����G��ʹOG��OD������GC��
�١�AFD���GCD�Ĺ�ϵ���� ������˵�����ɣ�
����ͼ3������AE��BE������ACB��45����CE��4�����߶�AE�ij��ȣ�
���𰸡���1����AFD����BCE����2���١�AFD��![]() ��GCD���AFD+��GCD��180������2
��GCD���AFD+��GCD��180������2![]() +2
+2![]() ��
��
��������
��1�����жϳ���BCE����ACD�������������ε��ڽǺͶ������жϳ���ACD����AFD�����ɵó����ۣ�
��2�������жϳ���ACD�ǵȱ������Σ��ó�AD��CD�����жϳ���ACD����AFD�������жϳ���AOD�ա�COG��SAS�����ó�AD��CG�����ɵó����ۣ�
�����жϳ���GCB����BCE�������жϳ���GCB����ACE�������жϳ���GCB�ա�ACE���ó�BC��CE��4�������������Ǻ������ɵó����ۣ�
�⣺��1����ͼ1��

AF��CD�Ľ��������N������ת֪����ACB����DCE����A����D��
���BCE����ACD��
�ߡ�ACD��180������A����ANC����AFD��180������D����DNF����ANC����DNF��
���ACD����AFD��
���AFD����BCE��
�ʴ�Ϊ����AFD����BCE��
��2���١�AFD��![]() ��GCD����AFD+��GCD��180����
��GCD����AFD+��GCD��180����
���ɣ���ͼ2������AD������ת֪����CAB����CDE��CA��CD����ACD��60����

���ACD�ǵȱ������Σ���AD��CD��
�ߡ�AMC����DMF��
���ACM�ס�DFM��
���ACD����AFD��
��O��AC���е㣬
��AO��CO��
��OD��OG����AOD����COG��
���AOD�ա�COG��SAS����
��AD��CG��
��CG��CD��
���GCD��2��ACD��120����
���AFD��![]() ��GCD����AFD+��GCD��180����
��GCD����AFD+��GCD��180����
�ʴ�Ϊ����AFD��![]() ��GCD����AFD+��GCD��180����
��GCD����AFD+��GCD��180����
������֪����GCD��120������ACD����BCE��60����
���GCA����GCD����ACD��60����
���GCA����BCE��
�ߡ�GCB����GCA+��ACB����ACE����BCE+��ACB��
���GCB����ACE��
����֪��CG��CD��CD��CA��
��CG��CA��
��BC��EC��4��
���GCB�ա�ACE��SAS����
��GB��AE��
��CG��CD��OG��OD��
��CO��GD��
���COG����COB��90��
��Rt��BOC��BO��BCsin��ACB��2![]() ��CO��BCcos��ACB��2
��CO��BCcos��ACB��2![]() ��
��
��Rt��GOC��GO��COtan��GCA��2![]() ��
��
��GB��CO+BO��2![]() +2
+2![]() ��
��
��AE��2![]() +2
+2![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ij�������ϰ�ʱ��õĽ�ͨ���ߵ�����������ȡ�˲���������е��飬Ҫ�����ߴӡ�![]() �����г���
�����г���![]() ����ͥ������
����ͥ������![]() ����������
����������![]() ���綯����
���綯����![]() �����������ѡ����ѡ����õ�һ������е�������������Ƴ����²�����������ͳ��ͼ������ͳ��ͼ������ͳ��ͼ�ش��������⣮
�����������ѡ����ѡ����õ�һ������е�������������Ƴ����²�����������ͳ��ͼ������ͳ��ͼ������ͳ��ͼ�ش��������⣮
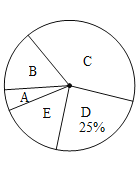
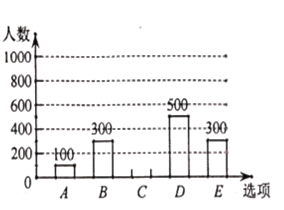
��1�����ε����У�һ�������� ����������ͳ��ͼ�У�![]() ���Ӧ������Բ�Ľ���_____
���Ӧ������Բ�Ľ���_____ ![]() ��
��
��2����ȫ����ͳ��ͼ��
��3�������ϰ�ʱ��![]() ���ֽ�ͨ���������ѡ��һ�֣� ���ϰ�ʱ��
���ֽ�ͨ���������ѡ��һ�֣� ���ϰ�ʱ��![]() ���ֽ�ͨ���������ѡ��һ�֣������б�������״ͼ�ķ���������ס������˶���ѡ
���ֽ�ͨ���������ѡ��һ�֣������б�������״ͼ�ķ���������ס������˶���ѡ![]() �ֽ�ͨ�����ϰ�ĸ��ʣ�
�ֽ�ͨ�����ϰ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�����������⣺
����һ��һ����λ���ϵ���Ȼ�����������Ȼ����ĩ��λ��ʾ������ĩ��λ֮ǰ�����ֱ�ʾ����֮����11�ı��������dz���������������С������������磺65362��362��65��297��11��27����65362�ǡ�����������
���϶������ε���Ȼ��p���ɷֽ�ΪP��100x+10y+z��x��0��0��y��9��0��z��9��x��y��z��Ϊ�������磺5278��52��100+10��7+8���涨��G��P����![]() ��
��
��1����֤������������������֮��һ���ܱ�11������
��2����֪��S��300+10b+a��t��1000b+100a+1142��1��a��7��0��b��5����a��b��Ϊ����������s+tΪ����������ʱ����G��t�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
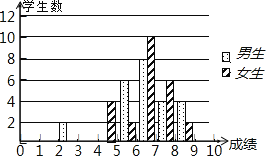
����Ŀ��Ϊ��ӭ�������п�������7���������ʦ��ȫ��48��ѧ��������һ������ģ����ԣ��÷־�Ϊ����������10�֣��ɼ��ﵽ6�����ϣ�����6�֣�Ϊ�ϸɼ��ﵽ9�����ϣ�����9�֣�Ϊ���㣬���ģ��������С�Ů��ȫ���ɼ��ֲ�������ͳ��ͼ����
��1���벹���������ijɼ�ͳ�Ʒ�������
ƽ���� | ���� | ��λ�� | �ϸ��� | ������ | |
���� | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
�� | ______ | 1.3 | ______ | 83.3% | 8.3% |
��2������˵���ǵĺϸ��ʡ������ʾ�����Ů�����������ǵijɼ�����Ů������Ů����ͬ��������˵������ΪŮ���ijɼ�Ҫ�������������������֧��Ů���۵�����ɣ�
��3��������ʦ˵���۰�ĺϸ��ʻ�����꣬��������̫�ͣ����DZ����ǿ�������������ܺ��Ŀ���ǣ�ȫ�������ʴﵽ50%�����Ů��������������ǡ������������������������������ô�С�Ů���ֱ��������������������ܴﵽ��ʦ��Ŀ�ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
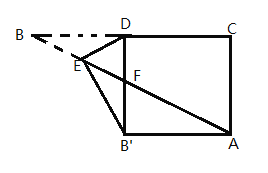
����Ŀ����ͼ,��![]() ��.
��.![]() ,
,![]() ,
,![]() ,��
,��![]() ��
��![]() ���е�,��
���е�,��![]() �DZ�
�DZ�![]() ��һ����,��
��һ����,��![]() ����ֱ�߰�
����ֱ�߰�![]() ���۵�
���۵�![]() ��λ��,
���,![]() ��
��![]() �ڵ�
�ڵ�![]() .��
.��![]() Ϊֱ��������,��
Ϊֱ��������,��![]() �ij�Ϊ_______��
�ij�Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
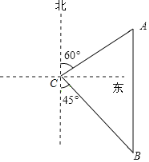
����Ŀ����ͼ��һ���ִ���λ�ڵ���![]() �ı�ƫ��60�����������60�����С��
�ı�ƫ��60�����������60�����С��![]() �����������Ϸ�����һ��ʱ�����λ�ڵ���
�����������Ϸ�����һ��ʱ�����λ�ڵ���![]() ����ƫ��45�������ϵ�
����ƫ��45�������ϵ�![]() ������ʱ�ִ�
������ʱ�ִ�![]() ��С��
��С��![]() �ľ�����__________���
�ľ�����__________���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��D��E�ֱ��Dz��ȱ�������ABC����AB��BC��AC���ı�AB��AC���е㣬O����ABC����ƽ���ϵĶ��㣬����OB��OC����G��F�ֱ���OB��OC���е㣬˳�����ӵ�D��G��F��E��

��1����ͼ������O����ABC���ڲ�ʱ����֤���ı���DGFE��ƽ���ı��Σ�
��2�����ı���DGFE�����Σ���O����λ��Ӧ����ʲô��������ֱ��д���𰸲���Ҫ˵�����ɣ���
��3����ͼ2��������O��ʹ���ı���DGFE�������Σ�������ͼ�ۼ�����д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ķ���A��B��x��ĸ������ϣ�����������y��![]() ��k1��0���ڵڶ������ڵ�ͼ��������ABCD�Ķ���D��m��2����BC���ϵĵ�G��n��
��k1��0���ڵڶ������ڵ�ͼ��������ABCD�Ķ���D��m��2����BC���ϵĵ�G��n��![]() ����ֱ��y=k2x+b��k2��0��������D����G����ʽ
����ֱ��y=k2x+b��k2��0��������D����G����ʽ![]() ��k2x+b�Ľ⼯Ϊ__________��
��k2x+b�Ľ⼯Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϲ�����������⣺��ͼ1����ƽ����һ������![]() ��ԭ��
��ԭ��![]() ��ʱ����ת��
��ʱ����ת��![]() �õ���һ������
�õ���һ������![]() ���
���![]() �ṹ��һ��ƽ��б����ϵ
�ṹ��һ��ƽ��б����ϵ![]()
�涨������![]() ��
��![]() ���ƽ���ߣ���
���ƽ���ߣ���![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ���ƽ���ߣ���
���ƽ���ߣ���![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ���Ӧ��ʵ��Ϊ
���Ӧ��ʵ��Ϊ![]() ����
����![]() ��
��![]() ���Ӧ��ʵ��Ϊ
���Ӧ��ʵ��Ϊ![]() ���������ʵ����
���������ʵ����![]() Ϊ��
Ϊ��![]() ��ƽ��б����ϵ
��ƽ��б����ϵ![]() �е�б���꣮��ͼ2����ƽ��б����ϵ
�е�б���꣮��ͼ2����ƽ��б����ϵ![]() �У���֪
�У���֪![]() ����
����![]() �������
�������![]() ����
����![]() �������
�������![]()
��1������![]() �����߶�
�����߶�![]() �ij���
�ij���
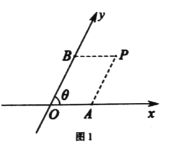
��2�����߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��
��![]() ����
����![]() ���
���![]() ��Ӧ�������
��Ӧ�������![]() ��б���ꣻ
��б���ꣻ
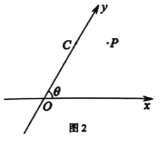
��3������![]() ��ֱ��
��ֱ��![]() ��һ���㣬��б����ϵ
��һ���㣬��б����ϵ![]() ȷ����ƽ�����Ե�
ȷ����ƽ�����Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶��
��Ϊ�뾶��![]() ������
������![]() ��
��![]() ������ʱ�����
������ʱ�����![]() ��б���꣬
��б���꣬
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com