Question

10．按照题意，画出图形，并计算：
（1）如图，点A、O、B在同一条直线上，画射线OD、OC、OE，使射线OD和射线OE分别平分∠AOC和∠BOC．（∠AOC和∠BOC都小于180°）；
（2）根据（1）中条件，若∠BOD=116°，求∠BOE的大小．

Answer 1

分析 （1）依照题意，画出图形即可；
（2）（方法一）根据角平分线的定义可得出∠AOD=∠COD=$\frac{1}{2}$∠AOC、∠COE=∠BOE=$\frac{1}{2}$∠BOC，根据邻补角互补结合∠BOD=116°可得出∠AOD的度数，进而可得出∠AOC、∠BOC的度数，再根据角平分线的定义即可得出∠BOE的度数；
（方法二）根据角平分线的定义结合邻补角互补可得出∠DOE=90°，将其代入∠BOE=∠BOD-∠DOE中可求出∠BOE的度数．

解答 解：（1）依照题意，画出图形．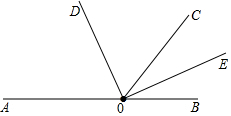
（2）（方法一）∵射线OD和射线OE分别平分∠AOC和∠BOC，
∴∠AOD=∠COD=$\frac{1}{2}$∠AOC，∠COE=∠BOE=$\frac{1}{2}$∠BOC．
∵∠BOD=116°，
∴∠AOD=180°-∠BOD=64°，
∴∠AOC=2∠AOD=128°．
∵∠AOC+∠BOC=180°，
∴∠BOC=52°，
∴∠BOE=$\frac{1}{2}$∠BOC=26°．
（方法二）∵射线OD和射线OE分别平分∠AOC和∠BOC，
∴∠AOD=∠COD=$\frac{1}{2}$∠AOC，∠COE=∠BOE=$\frac{1}{2}$∠BOC．
∵∠AOC+∠BOC=180°，
∴∠DOE=$\frac{1}{2}$（∠AOC+∠BOC）=90°，
∴∠BOE=∠BOD-∠DOE=26°．

点评 本题考查了角平分线的定义、邻补角以及角的计算，解题的关键是：（1）依照题意画出图形；（2）（方法一）根据角平分线的定义利用角的计算找出∠AOC、∠BOC的度数；（方法二）根据角平分线的定义结合邻补角互补找出∠DOE=90°．