
【题目】完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.求证:∠1=∠2.

证明:∵∠AED=∠C(已知),
∴ ∥ ( ),
∴∠B+∠BDE=180°( ),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴ ∥ ( ),
∴ ∠1=∠2( ).
【答案】DE;BC;同位角相等,两直线平行;两直线平行,同旁内角互补;EF;AB;同旁内角互补,两直线平行;两直线平行,内错角相等.
【解析】
先判断出DE∥BC得出∠B+∠BDE=180°,再等量代换,即可判断出EF∥AB,最后利用平行线的性质可得出结果.
解:∵∠AED=∠C(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠B+∠BDE=180°(两直线平行,同旁内角互补),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴EF∥AB(同旁内角互补,两直线平行),
∴∠1=∠2(两直线平行,内错角相等).
故答案为:DE;BC;同位角相等,两直线平行;两直线平行,同旁内角互补;EF;AB;同旁内角互补,两直线平行;两直线平行,内错角相等.


科目:初中数学 来源: 题型:
【题目】下列条件:①∠A﹣∠B=∠C; ②∠A:∠B:∠C=2:3:5; ③∠A=![]() ∠B=
∠B= ![]() ∠ C;④∠A=∠B=2∠C;⑤∠A=∠B=
∠ C;④∠A=∠B=2∠C;⑤∠A=∠B= ![]() ∠C,其中能确定△ABC 为直角三角形的条件有 ( )
∠C,其中能确定△ABC 为直角三角形的条件有 ( )
A.2 个B.3 个C.4 个D.5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
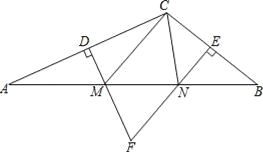
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
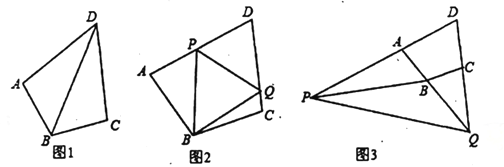
【题目】已知直线l1∥l2,且l4和l1、l2分别交于A、B两点,点P为线段AB上.的一个定点(如图1)

(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上.的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(不必说理由)
(3)如果点P在A、B两点外侧运动时, (点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不说理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形![]() 中,
中,![]() ,
,![]() .
.
(1)如图1.连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,满足
上,满足![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,如图3所示,仍然满足
的延长线上,如图3所示,仍然满足![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,并给出证明过程.
的数量关系,并给出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月26日,青盐铁路正式通车,作为沿线火车站之一的滨海港站带领滨海人民正式迈入了“高铁时代”,从盐城乘火车去北京的时间也大大缩短![]() 如图,OA、BC分别是普通列车和动车从盐城开往北京的路程
如图,OA、BC分别是普通列车和动车从盐城开往北京的路程![]() 与时间
与时间![]() 的函数图象
的函数图象![]() 请根据图中的信息,解答下列问题:
请根据图中的信息,解答下列问题:
![]() 根据图象信息,普通列车比动车早出发______h,动车的平均速度是______
根据图象信息,普通列车比动车早出发______h,动车的平均速度是______![]() ;
;
![]() 分别求出OA、BC的函数表达式,并写出自变量x的取值范围;
分别求出OA、BC的函数表达式,并写出自变量x的取值范围;
![]() 动车出发多少小时追上普通列车?此时他们距离出发地多少千米?
动车出发多少小时追上普通列车?此时他们距离出发地多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使![]() ,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为______度;
(2)在(1)旋转过程中,当旋转至图3的位置时,使得OM在∠BOC的内部,ON落在直线AB下方,试探究∠COM与∠BON之间满足什么等量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=3x+3交x轴于点A;直线y=-x平移后经过点B,交x轴于点C(7,0),另一直线y=kx-k交x轴于点D,交直线BC于点E,连接DB,BD⊥x轴.
(1)求直线BC的解析式和点B的坐标;
(2)若直线DE将△BDC的面积分为1:2的两部分,求k的值.
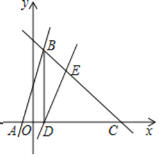
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com