
【题目】如图,直线AB:y=3x+3交x轴于点A;直线y=-x平移后经过点B,交x轴于点C(7,0),另一直线y=kx-k交x轴于点D,交直线BC于点E,连接DB,BD⊥x轴.
(1)求直线BC的解析式和点B的坐标;
(2)若直线DE将△BDC的面积分为1:2的两部分,求k的值.
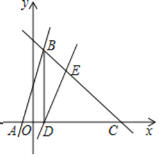
【答案】(1) y=-x+7, B(1,6);(2)2.
【解析】
(1)根据函数图象的平移“左加右减”即可解答
(2)点BD⊥x轴,即可得出点B的纵坐标为△BDC的高,只要求出点E,点D的坐标即可求出k值.
依题意,(1)由图解的平移可得直线BC的解析式为:y=-x+7,
∵直线AB与直线BC交于点B,有![]() ,
,
解得![]() ,故点B的坐标为(1,6);
,故点B的坐标为(1,6);
(2)由(1)得点B的坐标为(1,6),
∵BD⊥x轴,且点D在x轴上,
∴点D的坐标为(1,0),
∴|DC|=7-1=6,
∴![]() ,
,
∵直线DE将△BDC的面积分成1:2,
∴S△DEC:S△DBC=2:3,
∴![]() ,
,
∴在△DEC中有,过点E作EF⊥x轴,
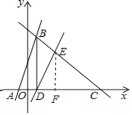
即EF为△DEC的高,
有![]() ,解得,EF=4,
,解得,EF=4,
又∵点E在直线BC上,将4代入y=-x+7得4=-x+7,
解得x=3,故点E的坐标为(3,4),
设直线DE的解析式为:y=kx+b,将点E,点D代入得![]() ,
,
解得![]() ,
,
故k的值为2.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.求证:∠1=∠2.

证明:∵∠AED=∠C(已知),
∴ ∥ ( ),
∴∠B+∠BDE=180°( ),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴ ∥ ( ),
∴ ∠1=∠2( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.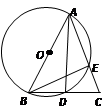
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】榴莲是热带著名水果之一,榴莲营养极为丰富,含有蛋白质、糖类、多种维生素、膳食纤维、脂肪、叶酸,氨基酸和矿物质,有强身健体、滋阴补阳之功效.它的气味浓烈、爱之者赞其香,厌之者怨其臭,喜欢榴莲的人也喜欢榴莲干,榴莲千层,榴莲披萨、榴莲酥等榴莲加工制品,某校数学兴趣小组为了了解本校学生喜爱榴莲的情况,随机抽取了200名学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:每一位同学在任何一种分类统计中只有一种选择)

请根据统计图完成下列问题:
(1)扇形统计图中,“很喜欢”所对应的圆心角度数为______度;喜欢榴莲千层的人数为______人;请补全条形统计图.
(2)若该校学生人数为8000人,请根据上述调查结果,估计该校学生中最爱吃榴莲干和榴莲酥的人数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)求表示户外活动时间1小时的扇形圆心角的度数;
(4)本次调查中学生参加户外活动的平均时间是否符合要求?户外活动时间的众数和中位数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD、CD.
(1)求证:AD=CD;
(2)①画图:在AC边上找一点H,使得BH+EH最小(要求:写出作图过程并画出图形,不用说明作图依据);
②当BC=2时,求出BH+EH的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一,点![]() 在线段
在线段![]() 上,图中有三条线段
上,图中有三条线段![]() 、
、![]() 和
和![]() ,若其中一条线段的长度是另外一条线段长度的
,若其中一条线段的长度是另外一条线段长度的![]() 倍,则称点
倍,则称点![]() 是线段
是线段![]() 的“巧点”.
的“巧点”.
(1)填空:线段的中点 这条线段的巧点(填“是”或“不是”或“不确定是”)
(问题解决)
(2)如图二,点![]() 和
和![]() 在数轴上表示的数分别是
在数轴上表示的数分别是![]() 和
和![]() ,点
,点![]() 是线段
是线段![]() 的巧点,求点
的巧点,求点![]() 在数轴上表示的数。
在数轴上表示的数。
(应用拓展)
(3)在(2)的条件下,动点![]() 从点
从点![]() 处,以每秒
处,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 向点
向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 向点
向点![]() 匀速运动,当其中一点到达中点时,两个点运动同时停止,当
匀速运动,当其中一点到达中点时,两个点运动同时停止,当![]()
![]() 、
、![]() 三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间
三点中,其中一点恰好是另外两点为端点的线段的巧点时,直接写出运动时间![]() 的所有可能值.
的所有可能值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com