
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= . 
【答案】![]()
【解析】解:连接OM,OC, 
∵OB=OC,且∠ABC=30°,
∴∠BCO=∠ABC=30°,
∵∠AOC为△BOC的外角,
∴∠AOC=2∠ABC=60°,
∵MA,MC分别为圆O的切线,
∴MA=MC,且∠MAO=∠MCO=90°,
在Rt△AOM和Rt△COM中,
![]() ,
,
∴Rt△AOM≌Rt△COM(HL),
∴∠AOM=∠COM= ![]() ∠AOC=30°,
∠AOC=30°,
在Rt△AOM中,OA= ![]() AB=1,∠AOM=30°,
AB=1,∠AOM=30°,
∴tan30°= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:AM= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了含30度角的直角三角形和切线的性质定理的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
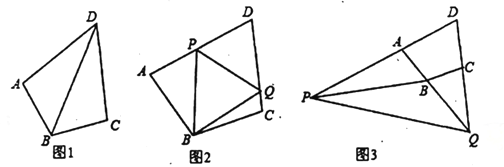
【题目】已知在四边形![]() 中,
中,![]() ,
,![]() .
.
(1)如图1.连接![]() ,若
,若![]() ,求证:
,求证:![]() .
.
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,满足
上,满足![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,如图3所示,仍然满足
的延长线上,如图3所示,仍然满足![]() ,请写出
,请写出![]() 与
与![]() 的数量关系,并给出证明过程.
的数量关系,并给出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.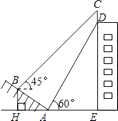
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初202l届数学组的老师们为了拍摄《燃烧我的数学》的MTV,从全年级选了m人(m>200)进行队列变换,现把m人排成一个10排的矩形队列,每排人数相等,然后把这个矩形队列平均分成A、B两个队列,如果从A队列中抽调36人到B队列,这样A、B队列都可以形成一个正方形队列,则m的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=3x+3交x轴于点A;直线y=-x平移后经过点B,交x轴于点C(7,0),另一直线y=kx-k交x轴于点D,交直线BC于点E,连接DB,BD⊥x轴.
(1)求直线BC的解析式和点B的坐标;
(2)若直线DE将△BDC的面积分为1:2的两部分,求k的值.
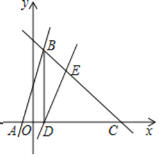
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.

(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=30°,求∠MGN+∠MPN的度数;
(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4 ![]() 米.
米.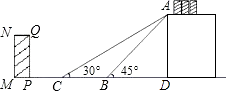
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列式子的因式分解做法:
①x2-1=(x-1)(x+1);
②x3﹣1
=x3﹣x+x﹣1
=x(x2﹣1)+x﹣1
=x(x﹣1)(x+1)+(x﹣1)
=(x﹣1)[x(x+1)+1]
=(x﹣1)(x2+x+1);
③x4﹣1
=x4﹣x+x﹣1
=x(x3﹣1)+x﹣1
=x(x﹣1)(x2+x+1)+(x﹣1)
=(x﹣1)[x(x2+x+1)+1]
=(x﹣1)(x3+x2+x+1);
…
(1)模仿以上做法,尝试对x5﹣1进行因式分解;
(2)观察以上结果,猜想xn﹣1= ;(n为正整数,直接写结果,不用验证)
(3)根据以上结论,试求45+44+43+42+4+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.(在括号中注明理由)
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD,(已知)
∴∠2=∠C,( )
又∵∠A=∠1,(已知)
∴AC∥ ,( )
∴∠2= ,( )
∴∠C=∠E(等量代换)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com