
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.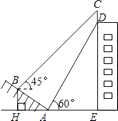
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() )
)
【答案】
(1)解:过B作BG⊥DE于G,

Rt△ABF中,i=tan∠BAH= ![]()
∴∠BAH=30°,∴BH= ![]() AB=5;
AB=5;
(2)解:由(1)得:BH=5,AH=5 ![]() ,∴BG=AH+AE=5
,∴BG=AH+AE=5 ![]() +15,
+15,
Rt△BGC中,∠CBG=45°,∴CG=BG=5 ![]() +15.
+15.
Rt△ADE中,∠DAE=60°,AE=15,∴DE= ![]() AE=15
AE=15 ![]() .
.
∴CD=CG+GE﹣DE=5 ![]() +15+5﹣15
+15+5﹣15 ![]() =20﹣10
=20﹣10 ![]() ≈2.7m.
≈2.7m.
答:宣传牌CD高约2.7米.
【解析】(1)在Rt△ABH中,根据AB的坡度求出∠BAH的度数,就可求出BH的长。
(2)在△ADE利用解直角三角形求出DE的长,进而可求出EH,即BG的长,然后在Rt△CBG中,∠CBG=45°,则CG=BG,由此可求出CG的长然后根据CD=CG+GE-DE即可求出宣传牌的高度。
【考点精析】利用解直角三角形和关于坡度坡角问题对题目进行判断即可得到答案,需要熟知解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法);坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B(a,b)是第一象限内一点,且a、b满足等式a2-6a+9+|b-1|=0.

(1)求点B的坐标;
(2)如图,动点C以每秒1个单位长度的速度从O点出发,沿x轴的正半轴方向运动,同时动点A以每秒2个单位长度的速度从O点出发,沿y轴的正半轴方向运动,设运动的时间为t秒,当t为何值时,△ABC是AB为斜边的等腰直角三角形;
(3)如图,在(2)的条件下,作∠ABC的平分线BD,设BD的长为m,△ADB的面积为S.请用含m的式子表示S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径为1的⊙A的圆心与坐标原点O重合,线段BC的端点分别在x轴与y轴上,点B的坐标为(6,0),且sin∠OCB= ![]() .
.
(1)若点Q是线段BC上一点,且点Q的横坐标为m.
①求点Q的纵坐标;(用含m的代数式表示)
②若点P是⊙A上一动点,求PQ的最小值;
(2)若点A从原点O出发,以1个单位/秒的速度沿折线OBC运动,到点C运动停止,⊙A随着点A的运动而移动.
①点A从O→B的运动的过程中,若⊙A与直线BC相切,求t的值;
②在⊙A整个运动过程中,当⊙A与线段BC有两个公共点时,直接写出t满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:问题:某班在购买啦啦操比赛的物资时,准备购买红色、黄色,蓝色三种颜色的啦啦球,其颜色不同则价格不同,第一次买了15个红色啦啦球、7个黄色啦啦球、11个蓝色啦啦球共用1084元,第二次买了2个红色啦啦球、4个黄色啦啦球、3个蓝色啦啦球共用304元,试问第三次买了红、黄、蓝啦啦球各一个共需多少元?(假定三次购买红、黄、蓝啦啦球单价不变)
解:设购买红、黄、蓝啦啦球的单价分别为x、y、z元,依题意得:
![]()
上述方程组可变形为:![]()
设x+y+z=m,2x+z=n,上述方程组又可化为:![]()
①+4×②得:m= ,即x+y+z= ;
答:第三次购买红、黄、蓝啦啦球各一个共需 元.
阅读后,细心的你,可以解决下列问题:
某同学买13支黑笔、5支红笔、9个笔记本,共用去92.5元:如果买2支黑笔、4支红笔、3个笔记本,则共用去32元,试问只买一支黑笔、一支红笔、一个笔记本,共需多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.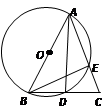
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com