
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.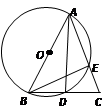
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ![]() ,求⊙O的半径。
,求⊙O的半径。
【答案】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90° 即AD是底边BC上的高.
又∵AB=AC,
∴△ABC是等腰三角形,
∴D是BC的中点
(2)证明:∵∠CBE与∠CAD是同弧所对的圆周角,
∴ ∠CBE=∠CAD.
又∵∠BCE=∠ACD,
∴△BEC∽△ADC;
(3)证明:由△BEC∽△ADC得: ![]() , 即CD·BC=AC·CE.
, 即CD·BC=AC·CE.
∵D是BC的中点,
∴CD= BC.
又∵AB=AC,∴CD·BC=AC·CE= ![]() BC ·BC=AB·CE 即BC
BC ·BC=AB·CE 即BC ![]() =2AB·CE=12
=2AB·CE=12
∴AB=6
∴⊙O的半径为3
【解析】(1)由AB是⊙O的直径,证出AD是底边BC上的高.根据等腰三角形三线合一的性质得出结论。
(2)根据同弧所对的圆周角相等,得出∠CBE=∠CAD,再根据两组角对应相等的两三角形相似。
(3)由△BEC∽△ADC得出对应边成比例,即可求出圆的半径。
【考点精析】本题主要考查了等腰三角形的性质和圆周角定理的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使![]() ,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为______度;
(2)在(1)旋转过程中,当旋转至图3的位置时,使得OM在∠BOC的内部,ON落在直线AB下方,试探究∠COM与∠BON之间满足什么等量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.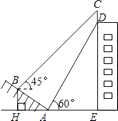
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是具有![]() 多年历史的古城扬州市区内的几个旅游景点分布示意图. 已知竹西公园的位置坐标为(300,300)(小正方形的边长代表100 m长). 则荷花池的坐标为________;平山堂的坐标为___________;汪氏小苑的坐标为___________.
多年历史的古城扬州市区内的几个旅游景点分布示意图. 已知竹西公园的位置坐标为(300,300)(小正方形的边长代表100 m长). 则荷花池的坐标为________;平山堂的坐标为___________;汪氏小苑的坐标为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初202l届数学组的老师们为了拍摄《燃烧我的数学》的MTV,从全年级选了m人(m>200)进行队列变换,现把m人排成一个10排的矩形队列,每排人数相等,然后把这个矩形队列平均分成A、B两个队列,如果从A队列中抽调36人到B队列,这样A、B队列都可以形成一个正方形队列,则m的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=3x+3交x轴于点A;直线y=-x平移后经过点B,交x轴于点C(7,0),另一直线y=kx-k交x轴于点D,交直线BC于点E,连接DB,BD⊥x轴.
(1)求直线BC的解析式和点B的坐标;
(2)若直线DE将△BDC的面积分为1:2的两部分,求k的值.
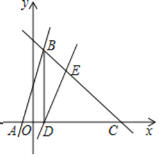
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4 ![]() 米.
米.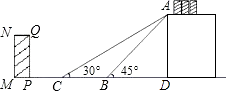
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于新冠肺炎病毒肆虐全球,市面上 KN95 等防护型口罩出现热销.武汉市某学校准备购进一批口罩,已知 3 个 A 型口罩和 2 个 B 型口罩共需 95 元;10 个 A 型口罩和 5 个 B 型口罩共需 250 元.
(1)求一个 A 型口罩和一个 B 型口罩的售价各是多少元;
(2)学校准备购进这两种型号的口罩共 500 个,正好赶上药店对口罩价格进行调整,其中 A 型口罩售价比原价提高 7 元,B 型口罩按原价九五折出售,若学校此次购买两种口罩的总费用不超过 10000 元,且保证购买的 B 型口罩数量不少于135 个,请设计出最省钱的购买方案,并给出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com