
����Ŀ�������¹ڷ��ײ�����Űȫ�������� KN95 �ȷ����Ϳ��ֳ����������人��ijѧУ������һ�����֣���֪ 3 �� A �Ϳ��ֺ� 2 �� B �Ϳ��ֹ��� 95 Ԫ��10 �� A �Ϳ��ֺ� 5 �� B �Ϳ��ֹ��� 250 Ԫ��
(1)��һ�� A �Ϳ��ֺ�һ�� B �Ϳ��ֵ��ۼ۸��Ƕ���Ԫ��
(2)ѧУ�������������ͺŵĿ��ֹ� 500 �������ø���ҩ��Կ��ּ۸���е��������� A �Ϳ����ۼ۱�ԭ����� 7 Ԫ��B �Ϳ��ְ�ԭ�۾����۳��ۣ���ѧУ�˴ι������ֿ��ֵ��ܷ��ò����� 10000 Ԫ���ұ�֤����� B �Ϳ�������������135 ��������Ƴ���ʡǮ�Ĺ�������������ͷ��ã�
���𰸡���1��A�Ϳ���ÿ��5Ԫ��B�Ϳ���ÿ��40Ԫ����2������A�Ϳ���365����B�Ϳ���135������ͷ���Ϊ9510Ԫ��
��������
��1����һ�� A �Ϳ���xԪ��һ�� B �Ϳ���yԪ������������ϵ�г���Ԫһ�η������ɣ�
��2���蹺��B�Ϳ���a��������ΪWԪ�������һ�� A �Ϳ��ֺ�һ�� B �Ϳ������ڵ��ۼۣ����ݲ��ȹ�ϵ�г�����ʽ�����a��ȡֵ��Χ���ú���a�Ĵ���ʽ��ʾ��W������һ�κ����������Խ���Ա�����ȡֵ��Χ���ɽ��
��1����һ�� A �Ϳ���xԪ��һ�� B �Ϳ���yԪ����������ã�
![]()
��ã�![]()
��һ��A�Ϳ����ۼ���5Ԫ��һ��B�Ϳ���40Ԫ��
��2���蹺��B�Ϳ���a��������ΪWԪ����
һ��A�Ϳ������ۼۣ�5+7=12Ԫ
һ��B�Ϳ������ۼۣ�40��0.95=38Ԫ
��������ã�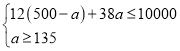
��ã�![]()
W=![]()
W��a��һ�κ�������W��a����������ʵ�a=135ʱW��С��
W��С=26��135+600=9510Ԫ
��ʱ����A�Ϳ���365����B�Ϳ���135����
����ʡǮ�Ĺ���Ϊ������A�Ϳ���365����B�Ϳ���135������ͷ���Ϊ9510Ԫ��


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABΪֱ���ġ�O��AC��E����BC��D��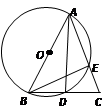
��1��D��BC���е㣻
��2����BEC�ס�ADC��
��3���� ![]() �����O�İ뾶��
�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90������BAC��30����EΪAB�ߵ��е㣬��BEΪ�����ȱ���BDE������AD��CD��
��1����֤��AD��CD��
��2���ٻ�ͼ����AC������һ��H��ʹ��BH+EH��С��Ҫ��д����ͼ���̲�����ͼ�Σ�����˵����ͼ���ݣ���
�ڵ�BC��2ʱ�����BH+EH����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����O�İ뾶Ϊ5����BC=8����A�ǡ�O��һ�㣬��AB=AC��ֱ��AO��BC���ڵ�D����AD�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1�����㣺��3���У�0+���� ![]() ����2+
����2+ ![]() ��2|sin45�㩁1|��
��2|sin45�㩁1|��
��2���Ȼ�������ֵ�� ![]() ������ʵ��mʹ����x��һԪ���η���x2��4x��m=0��������ȵ�ʵ������
������ʵ��mʹ����x��һԪ���η���x2��4x��m=0��������ȵ�ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ӵ����ϵĵ�A��һɽ���ϵĵ��߸�PQ����ø˶��˵�P��������45�㣬��ǰ��9m����B�㣬��ø˶��˵�P�˵˵�Q�����Ƿֱ���60���30�㣮
��1�����BPQ�Ķ�����
��2����õ��߸�PQ�ĸ߶ȣ�������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼһ����![]() ���߶�
���߶�![]() �ϣ�ͼ���������߶�
�ϣ�ͼ���������߶�![]() ��
��![]() ��
��![]() ��������һ���߶εij���������һ���߶γ��ȵ�
��������һ���߶εij���������һ���߶γ��ȵ�![]() ������Ƶ�
������Ƶ�![]() ���߶�
���߶�![]() �ġ��ɵ㡱��
�ġ��ɵ㡱��
��1����գ��߶ε��е� �����߶ε��ɵ㣨��ǡ����ǡ���ȷ���ǡ���
����������
��2����ͼ������![]() ��
��![]() �������ϱ�ʾ�����ֱ���
�������ϱ�ʾ�����ֱ���![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() ���ɵ㣬���
���ɵ㣬���![]() �������ϱ�ʾ������
�������ϱ�ʾ������
��Ӧ����չ��
��3���ڣ�2���������£�����![]() �ӵ�
�ӵ�![]() ������ÿ��
������ÿ��![]() ����λ���ٶ���
����λ���ٶ���![]() ���
���![]() �����˶���ͬʱ����
�����˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ٶ���
����λ���ٶ���![]() ���
���![]() �����˶���������һ�㵽���е�ʱ���������˶�ͬʱֹͣ����
�����˶���������һ�㵽���е�ʱ���������˶�ͬʱֹͣ����![]()
![]() ��
��![]() �����У�����һ��ǡ������������Ϊ�˵���߶ε��ɵ�ʱ��ֱ��д���˶�ʱ��
�����У�����һ��ǡ������������Ϊ�˵���߶ε��ɵ�ʱ��ֱ��д���˶�ʱ��![]() �����п���ֵ��
�����п���ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�Ҫѡ���ס�������������������������10�����������12��������Ҫ2100Ԫ���������������5�����������8��������Ҫ1250Ԫ��
��1����ס����������ÿ���ֱ�Ϊ����Ԫ��
��2����ÿ��������������ۼ۸�Ϊ108Ԫ��ÿ��������������ۼ۸�Ϊ140Ԫ�������г������̵������������������������ȹ������������������3������2�����������ȫ���۳���Ҫʹ�ܻ�������976Ԫ������Ӧ��������������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У�AB��AC����DΪBC�е㣮��MDN��90������MDN�Ƶ�D��ת��DM��DN�ֱ����AB��AC����E��F���㣮���н��ۣ�
����DEF�ǵ���ֱ�������Σ�
��AE��CF��
����BDE�ա�ADF��
��BE+CF��EF��
��S�ı���AEDF��![]() AD2��
AD2��
������ȷ������_____������ţ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com