
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD、CD.
(1)求证:AD=CD;
(2)①画图:在AC边上找一点H,使得BH+EH最小(要求:写出作图过程并画出图形,不用说明作图依据);
②当BC=2时,求出BH+EH的最小值.

【答案】(1)证明见解析;(2)①画图见解析;②EH+HB的最小值=2![]() .
.
【解析】
(1)证明△ABC≌△ABD(SAS),可得AC=AD.
(2)①作点B关于直线AC的对称点B′,连接EB′交AC于H,点H即为所求;②连接AB′,证明△ABB′是等边三角形即可解决问题.
(1)证明:∵∠ACB=90°,∠BAC=30°,
∴AB=2BC,∠ABC=60°
∵AE=EB,
∴BC=BE,
∵△BED是等边三角形,
∴BE=BD,∠ABD=60°,
∵AB=AB,∠ABC=∠ABD=60°,BC=BD,
∴△ABC≌△ABD(SAS),
∴AC=AD.
(2)①作点B关于直线AC的对称点B′,连接EB′交AC于H,点H即为所求.

②连接AB′,
∵AC⊥BB′,CB=CB′,
∴AB=AB′,
∵∠ABC=60°,
∴△ABB′是等边三角形,
∵AE=EB,
∴B′E⊥AB,
在Rt△BEB′中,∵BB′=4,∠EBB′=60°,
∴EB′=BB′sin60°=2![]() ,
,
∴EH+HB的最小值=EH+HB′=EB′=2![]()


科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使![]() ,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
,将一直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为______度;
(2)在(1)旋转过程中,当旋转至图3的位置时,使得OM在∠BOC的内部,ON落在直线AB下方,试探究∠COM与∠BON之间满足什么等量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=3x+3交x轴于点A;直线y=-x平移后经过点B,交x轴于点C(7,0),另一直线y=kx-k交x轴于点D,交直线BC于点E,连接DB,BD⊥x轴.
(1)求直线BC的解析式和点B的坐标;
(2)若直线DE将△BDC的面积分为1:2的两部分,求k的值.
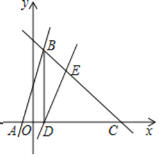
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4 ![]() 米.
米.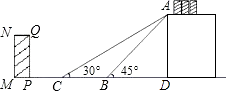
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,同底数幂的乘法法则为am·an=am+n(其中a≠0 ,m、n为正整数),类似地我们规定关于任意正整数m、n的一种新运算:h(m+n)=h(m)·h(n);比如h(2)=3,则h(4)=h(2+2)=3×3=9,若h(2)=k(k≠0 ),那么h(2n)·h(2020)的结果是( )
A.2k+2020B.2k+1010C.kn+1010D.1022k
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列式子的因式分解做法:
①x2-1=(x-1)(x+1);
②x3﹣1
=x3﹣x+x﹣1
=x(x2﹣1)+x﹣1
=x(x﹣1)(x+1)+(x﹣1)
=(x﹣1)[x(x+1)+1]
=(x﹣1)(x2+x+1);
③x4﹣1
=x4﹣x+x﹣1
=x(x3﹣1)+x﹣1
=x(x﹣1)(x2+x+1)+(x﹣1)
=(x﹣1)[x(x2+x+1)+1]
=(x﹣1)(x3+x2+x+1);
…
(1)模仿以上做法,尝试对x5﹣1进行因式分解;
(2)观察以上结果,猜想xn﹣1= ;(n为正整数,直接写结果,不用验证)
(3)根据以上结论,试求45+44+43+42+4+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上原点为0,点B表示的数为2,A在B的右边,且A与B的距离为5,,动点P从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点Q从点A出发,以每秒4个单位长度的速度向左匀速运动。设运动时间为t秒(t>0).
![]()
(1)写出数轴上点A表示的数 ,点P表示的数 (用含t的代数式表示),点Q表示的数(用含t的代数式表示);
(2)问点P与点Q何时到点O的距离相等?
(3)若点D是数轴上一点,点D表示的数是x,是否存在x,使得![]() ?如果存在,请直接写出x的值;如果不存在,说明理由.
?如果存在,请直接写出x的值;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于新冠肺炎病毒肆虐全球,市面上 KN95 等防护型口罩出现热销.武汉市某学校准备购进一批口罩,已知 3 个 A 型口罩和 2 个 B 型口罩共需 95 元;10 个 A 型口罩和 5 个 B 型口罩共需 250 元.
(1)求一个 A 型口罩和一个 B 型口罩的售价各是多少元;
(2)学校准备购进这两种型号的口罩共 500 个,正好赶上药店对口罩价格进行调整,其中 A 型口罩售价比原价提高 7 元,B 型口罩按原价九五折出售,若学校此次购买两种口罩的总费用不超过 10000 元,且保证购买的 B 型口罩数量不少于135 个,请设计出最省钱的购买方案,并给出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商城销售![]() 、
、![]() 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为![]() 元、
元、![]() 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:
销售时段 | 销售型号 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 、
、![]() 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若商城准备用不多于![]() 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共![]() 台,求
台,求![]() 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?
(3)在(2)的条件下商城销售完这![]() 台电风能否实现利润超过
台电风能否实现利润超过![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com