
【题目】某商店要选购甲、乙两种零件,若购进甲种零件10件,乙种零件12件,共需要2100元;若购进甲种零件5件,乙种零件8件,共需要1250元.
(1)求甲、乙两种零件每件分别为多少元?
(2)若每件甲种零件的销售价格为108元,每件乙种零件的销售价格为140元,根据市场需求,商店决定,购进甲种零件的数量比购进乙种零件的数量的3倍还多2件,这样零件全部售出后,要使总获利超过976元,至少应购进乙种零件多少件?
【答案】(1)甲种零件的单价是90元/件,乙种零件的单价是100元/件;(2)至少应购进乙种零件11件.
【解析】
(1)设甲种零件的单价是x元/件,乙种零件的单价是y元/件,根据“购进甲种零件10件,乙种零件12件,共需要2100元;若购进甲种零件5件,乙种零件8件,共需要1250元”列出方程组并解答;
(2)设该商店本次购进乙种零件m个,则购进甲种零件![]() 个,根据“总利润=单个利润×销售数量”,结合总获利大于976元,即可得出关于m的一元一次不等式,解之取其中的最小整数值即可得出结论.
个,根据“总利润=单个利润×销售数量”,结合总获利大于976元,即可得出关于m的一元一次不等式,解之取其中的最小整数值即可得出结论.
(1)设甲种零件的单价是x元/件,乙种零件的单价是y元/件
由题意得![]()
解得![]()
答:甲种零件的单价是90元/件,乙种零件的单价是100元/件;
(2)设该商店本次购进乙种零件m个,则购进甲种零件![]() 个
个
由题意得![]()
解得![]()
因为m是整数
所以m最小值是11
答:至少应购进乙种零件11件.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4 ![]() 米.
米.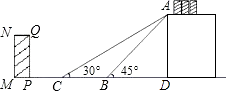
(1)求新传送带AC的长度.
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.
参考数据: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于新冠肺炎病毒肆虐全球,市面上 KN95 等防护型口罩出现热销.武汉市某学校准备购进一批口罩,已知 3 个 A 型口罩和 2 个 B 型口罩共需 95 元;10 个 A 型口罩和 5 个 B 型口罩共需 250 元.
(1)求一个 A 型口罩和一个 B 型口罩的售价各是多少元;
(2)学校准备购进这两种型号的口罩共 500 个,正好赶上药店对口罩价格进行调整,其中 A 型口罩售价比原价提高 7 元,B 型口罩按原价九五折出售,若学校此次购买两种口罩的总费用不超过 10000 元,且保证购买的 B 型口罩数量不少于135 个,请设计出最省钱的购买方案,并给出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.(在括号中注明理由)
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD,(已知)
∴∠2=∠C,( )
又∵∠A=∠1,(已知)
∴AC∥ ,( )
∴∠2= ,( )
∴∠C=∠E(等量代换)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商城销售![]() 、
、![]() 两种型号的电风扇,进价分别为
两种型号的电风扇,进价分别为![]() 元、
元、![]() 元,下表是近两周的销售情况:
元,下表是近两周的销售情况:
销售时段 | 销售型号 | 销售收入 | |
|
| ||
第一周 |
|
|
|
第二周 |
|
|
|
(1)求![]() 、
、![]() 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若商城准备用不多于![]() 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共![]() 台,求
台,求![]() 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?
(3)在(2)的条件下商城销售完这![]() 台电风能否实现利润超过
台电风能否实现利润超过![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣3x+k与x轴交于A、B两点,与y轴交于点C(0,﹣4).
(1)k=;
(2)点A的坐标为 , B的坐标为;
(3)设抛物线y=x2﹣3x+k的顶点为M,求四边形ABMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 ![]() (元)与销售单价
(元)与销售单价 ![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com