Question

【题目】如图，抛物线y=x2﹣3x+k与x轴交于A、B两点，与y轴交于点C（0，﹣4）．

（1）k=；
（2）点A的坐标为 ， B的坐标为；
（3）设抛物线y=x2﹣3x+k的顶点为M，求四边形ABMC的面积．

Answer 1

【答案】
（1）k=﹣4
（2）（﹣1,0）,（4,0）
（3）解：∵y=x2﹣3x﹣4=

∴ ，

设抛物线的对称轴与x轴交于N，如图所示：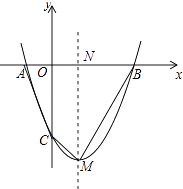

则四边形ABMC的面积=S△ACN+S△NCM+S△NMB

=

=

=

∴四边形ABMC的面积是 ．

【解析】

解：（1）把点C（0，﹣4）代入抛物线y=x2﹣3x+k得：k=﹣4，

所以答案是：k=﹣4；（2）∵y=x2﹣3x﹣4，

当y=0时，x2﹣3x﹣4=0，

解得：x=﹣1，或x=4，

∴A（﹣1，0），B（4，0）；

所以答案是：（﹣1，0），（4，0）；

【考点精析】掌握二次函数图象的平移和抛物线与坐标轴的交点是解答本题的根本，需要知道平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减；一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．