
【题目】初202l届数学组的老师们为了拍摄《燃烧我的数学》的MTV,从全年级选了m人(m>200)进行队列变换,现把m人排成一个10排的矩形队列,每排人数相等,然后把这个矩形队列平均分成A、B两个队列,如果从A队列中抽调36人到B队列,这样A、B队列都可以形成一个正方形队列,则m的值为______.
【答案】650
【解析】
根据已知设总人数为10x,进而得出5x+36和5x-36都是完全平方数,再利用a2-b2=(a+b)(a-b)=72=1×72=2×36=3×24=4×18=6×12=8×9,得出所有符合要求的a,b的值,进而得出总人数.
设总人数为10x人,利用平均分成A、B两个队列,如果从A队列中抽调36人到B队列,这样A、B队列都可以形成一个正方形队列,
得出:5x+36和5x-36都是完全平方数,设它们分别是a2和b2,
a2-b2=(a+b)(a-b)=72=1×72=2×36=3×24=4×18=6×12=8×9,
得(a,b)为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
解得:a=36.5,b=35.5或a=19,b=17或a=13.5,b=10.5或a=11,b=7或a=9,b=3或a=8.5,b=0.5,
故所有的a,b值为:(36.5,35.5),(19,17),(13.5,10.5),(11,7),(9,3),(8.5,0.5),
显然只有(19,17),(11,7),(9,3)符合,
∴5x+36等于361或121或81,
∴人数=10x=(361-36)×2=650或10x=(121-36)×2=170或10x=(81-36)×2=90,
∵m>200,
∴m=650,
故答案为:650.


科目:初中数学 来源: 题型:
【题目】随着互联网技术的广泛应用,“天猫”、“京东”、“唯品会”等网络大型‘:卖场”的日趋完善,网购成了现代人生活的一部分。与此同时,快递行业也随之高速发展.
(1)如果每名快递员每月最多完成快递投递量相同,且每月投递完l2万件快递量需要快递员比投递完12.6万件快递置需要快递员人数少1人,求每名快递员每月最多完成快递投递量是多少万件;
(2)我市某小型快递公司原有员工20名,随着快递投递任务的加大,该快递公司投入部分资金用于改善投递条件,改善后,每人每月投递快递任务量可增加![]() ,同时该快递公司又增加了20%的快递员,从而预计每月最大可完成投递快递任务l5.12万件,求
,同时该快递公司又增加了20%的快递员,从而预计每月最大可完成投递快递任务l5.12万件,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:问题:某班在购买啦啦操比赛的物资时,准备购买红色、黄色,蓝色三种颜色的啦啦球,其颜色不同则价格不同,第一次买了15个红色啦啦球、7个黄色啦啦球、11个蓝色啦啦球共用1084元,第二次买了2个红色啦啦球、4个黄色啦啦球、3个蓝色啦啦球共用304元,试问第三次买了红、黄、蓝啦啦球各一个共需多少元?(假定三次购买红、黄、蓝啦啦球单价不变)
解:设购买红、黄、蓝啦啦球的单价分别为x、y、z元,依题意得:
![]()
上述方程组可变形为:![]()
设x+y+z=m,2x+z=n,上述方程组又可化为:![]()
①+4×②得:m= ,即x+y+z= ;
答:第三次购买红、黄、蓝啦啦球各一个共需 元.
阅读后,细心的你,可以解决下列问题:
某同学买13支黑笔、5支红笔、9个笔记本,共用去92.5元:如果买2支黑笔、4支红笔、3个笔记本,则共用去32元,试问只买一支黑笔、一支红笔、一个笔记本,共需多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.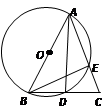
(1)D是BC的中点;
(2)△BEC∽△ADC;
(3)若 ![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边上,若AE=![]() ,AD=
,AD=![]() ,则BC的长为______.
,则BC的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com