
【题目】在△ABC中,∠A、∠B为锐角,且|tanA﹣1|+( ![]() ﹣cosB)2=0,则∠C=°.
﹣cosB)2=0,则∠C=°.
【答案】75
【解析】根据非负数的性质求出tanA和cosB的值,然后求出∠A、∠B的度数,最后求出∠C.
解:由题意得,tanA=1,cosB= ![]() ,
,
则∠A=45°,∠B=60°,
则∠C=180°﹣45°﹣60°=75°.
所以答案是:75.
【考点精析】掌握三角形的内角和外角和特殊角的三角函数值是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.


科目:初中数学 来源: 题型:
【题目】如图,给出下列四个条件:① ∠BAC=∠DCA;② ∠DAC=∠BCA;③ ∠ABD=∠CDB;④ ∠ADB=∠CBD,其中能使 AD∥BC的条件是( )

A.①②B.③④C.②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
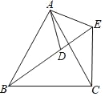
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )

A. 15 B. 12.5 C. 14.5 D. 17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全校学生对新闻,体育.动画、娱乐、戏曲五类电视节目的喜爱情况,机调查了100名学生,结果如扇形图所示,依据图中信息,回答下列问题: (1)在被调查的学生中,喜欢“动画”节目的学生有 _____(名); (2)在扇形统计图中,喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 _____(度).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初202l届数学组的老师们为了拍摄《燃烧我的数学》的MTV,从全年级选了m人(m>200)进行队列变换,现把m人排成一个10排的矩形队列,每排人数相等,然后把这个矩形队列平均分成A、B两个队列,如果从A队列中抽调36人到B队列,这样A、B队列都可以形成一个正方形队列,则m的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )
A. ∠ABD=∠ACE B. BD=CE C. ∠BAD=∠CAE D. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.

(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=30°,求∠MGN+∠MPN的度数;
(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连结OA,二次函数y=x2图象从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
(1)求线段OA所在直线的函数解析式;
(2)设二次函数顶点M的横坐标为m,当m为何值时,线段PB最短,并求出二次函数的表达式;
(3)当线段PB最短时,二次函数的图象是否过点Q(a,a﹣1),并说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]()
(1)求证:![]() 是等边三角形
是等边三角形
(2)如图2,在![]() 内有一点
内有一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的度数
的度数
(3)如图3,在(2)的条件下,在![]() 外有一点
外有一点![]() ,连接
,连接![]() 、
、![]() 、若
、若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com