
【题目】为了解全校学生对新闻,体育.动画、娱乐、戏曲五类电视节目的喜爱情况,机调查了100名学生,结果如扇形图所示,依据图中信息,回答下列问题: (1)在被调查的学生中,喜欢“动画”节目的学生有 _____(名); (2)在扇形统计图中,喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 _____(度).

科目:初中数学 来源: 题型:
【题目】如图,扇形OMN与正方形ABCD,半径OM与边AB重合,弧MN的长等于AB的长,已知AB=2,扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止,则点O经过的路径长 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,点E在边AD上,连接BE将△ABE沿BE翻折,得到△MBE,且点M是CD中点,取BM中点N,点P为线段BE上一动点,连接PN,PM,若AD长为2,则PM+PN的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实施“城乡危旧房改造工程”中,河西区计划推出A、B两种新户型![]() 根据预算,建成10套A种户型和30套B种户型住房共需资金480万元,建成30套A种户型和10套B种户型住房共需资金400万元
根据预算,建成10套A种户型和30套B种户型住房共需资金480万元,建成30套A种户型和10套B种户型住房共需资金400万元
![]() 在危旧房改造中建成一套A种户型和一套B种户型住房所需资金分别是多少万元?
在危旧房改造中建成一套A种户型和一套B种户型住房所需资金分别是多少万元?
![]() 河西区有800套住房需要改造,改造资金由国家危旧房补贴和地方财政共同承担,若国家补贴拨付的改造资金不少于2100万元,河西区财政投入额资金不超过7700万元,其中国家财政投入到A、B两种户型的改造资金分别为每套2万元和3万元
河西区有800套住房需要改造,改造资金由国家危旧房补贴和地方财政共同承担,若国家补贴拨付的改造资金不少于2100万元,河西区财政投入额资金不超过7700万元,其中国家财政投入到A、B两种户型的改造资金分别为每套2万元和3万元
![]() 请你计算求出A种户型至少可以建多少套?最多可以建多少套?
请你计算求出A种户型至少可以建多少套?最多可以建多少套?
![]() 设这项改造工程总投入资金W万元,建成A种户型m套,写出W与m的关系式,并求出最少总投入.
设这项改造工程总投入资金W万元,建成A种户型m套,写出W与m的关系式,并求出最少总投入.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空,并在括号内标注理由.
已知:如图①,DE∥BC,∠2=∠B,求证∠B+∠BFE=180°.
证明:∵DE![]() BC(已知),
BC(已知),
∴∠1=∠ ( ).
又∵∠2=∠B( 已知 ),∴∠ =∠ .
∴ EF![]() ( ).
( ).
∴∠B+∠BFE=180°( ).
(2)如图②,AB![]() CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.
CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.

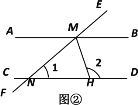
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(-1,2),C(-1,-2),D(1,-2),点M和点N同时从E(0,2)点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(m+1)x2﹣(m+3)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com