
【题目】(1)填空,并在括号内标注理由.
已知:如图①,DE∥BC,∠2=∠B,求证∠B+∠BFE=180°.
证明:∵DE![]() BC(已知),
BC(已知),
∴∠1=∠ ( ).
又∵∠2=∠B( 已知 ),∴∠ =∠ .
∴ EF![]() ( ).
( ).
∴∠B+∠BFE=180°( ).
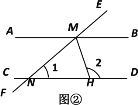
(2)如图②,AB![]() CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.
CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.

【答案】(1)见解析;(2)![]()
【解析】
(1)根据两直线平行,同位角相等可推出∠1=∠B,从而得出∠1=∠2,根据内错角相等,两直线平行推出EF∥AB,再根据两直线平行,同旁内角互补即可得出结论;
(2)根据两直线平行,同旁内角互补即可求出![]() ,再根据角平分线的定义求出
,再根据角平分线的定义求出![]() ,再根据两直线平行,同旁内角互补即可求出∠2.
,再根据两直线平行,同旁内角互补即可求出∠2.
证明:∵DE∥BC(已知),
∴∠1=∠ B ( 两直线平行同位角相等).
又∵∠2=∠B( 已知 ),∴∠ 1 =∠ 2 .
∴ EF∥ AB ( 内错角相等两直线平行).
∴∠B+∠BFE=180°( 两直线平行同旁内角互补).
(2)∵AB//CD,∠1=40° ,
∴![]() ,即
,即![]() ,
,
∵MH平分∠BMN,
∴![]() ,
,
∵AB//CD ,
∴![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】市场上的红茶由茶原液与纯净水按一定比例配制而成,其中购买一吨茶原液的钱可以买15 吨纯净水。由于今年以来茶产地连续大旱,茶原液收购价上涨50%.纯净水价也上涨了10%,导致配制的这种茶饮料成本上涨40%,问这种茶饮料中茶原液与纯净水的配制比例为_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从全校1200名学生中随机选取一部分学生进行调查,调查情况:A:上网时间 ![]() 小时;B:1小时<上网时间
小时;B:1小时<上网时间 ![]() 小时;C:4小时<上网时间
小时;C:4小时<上网时间 ![]() 小时;D:上网时间>7小时.统计结果制成了如图统计图:
小时;D:上网时间>7小时.统计结果制成了如图统计图:
(1)参加调查的学生有人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在 ![]() 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 ![]() 处飞出(
处飞出( ![]() 在
在 ![]() 轴上),运动员孙可在距
轴上),运动员孙可在距 ![]() 点6米的
点6米的 ![]() 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ![]() ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.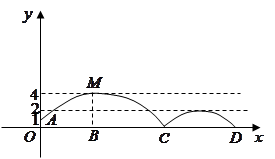
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 ![]() 距守门员多少米?(取
距守门员多少米?(取 ![]() )
)
(3)孙可要抢到足球第二个落地点 ![]() ,他应从第一次落地点
,他应从第一次落地点 ![]() 再向前跑多少米?(取
再向前跑多少米?(取 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全校学生对新闻,体育.动画、娱乐、戏曲五类电视节目的喜爱情况,机调查了100名学生,结果如扇形图所示,依据图中信息,回答下列问题: (1)在被调查的学生中,喜欢“动画”节目的学生有 _____(名); (2)在扇形统计图中,喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 _____(度).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,0)
B.(6,2)
C.(6,3)
D.(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )
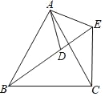
A. ∠ABD=∠ACE B. BD=CE C. ∠BAD=∠CAE D. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.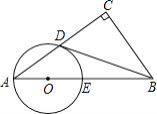
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com