
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.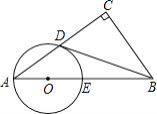
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
【答案】
(1)证明:连接OD、DE, 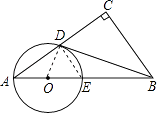
∵OA=OD,
∴∠A=∠ADO,
∵∠A+∠CDB=90°,
∴∠ADO+∠CDB=90°,
∴∠ODB=180°﹣90°=90°,
∴OD⊥BD,
∵OD是⊙O半径,
∴直线BD与⊙O相切;
(2)解:∵AE是⊙O直径,
∴∠ADE=90°=∠C,
∴BC∥DE,
∴△ADE∽△ACB,
∴ ![]()
∵D为AC中点,
∴AD=DC= ![]() AC,
AC,
∴AE=BE= ![]() AB,
AB,
DE是△ACB的中位线,
∴AE= ![]() AB,DE=
AB,DE= ![]() BC=
BC= ![]() ×6=3,
×6=3,
设AD=4a,AE=5a,
在Rt△ADE中,由勾股定理得:DE=3a=3,
解得:a=1,
∴AE=5a=5,
答:⊙O的直径是5.
【解析】(1)连接OD、DE,易证∠A=∠ADO,证出∠A+∠CDB=90°,得出∠ADO+∠CDB=90°,可得到OD⊥BD,根据切线的判定定理即可得出结论。
(2)根据圆周角定理得出∠ADE==∠C,从而证得BC∥DE,由平行得三角形相似得出△ADE∽△ACB,得出对应边成比例,再证明DE是△ACB的中位线,然后根据勾股定理建立方程求出a的值,即可求出圆的直径。
【考点精析】掌握勾股定理的概念和三角形中位线定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,与y轴交于点
,与y轴交于点![]() ,与x轴交于点C.
,与x轴交于点C.
![]() 求直线
求直线![]() 的函数表达式;
的函数表达式;
![]() 求
求![]() 的面积;
的面积;
![]() 在平面直角坐标系中有一点
在平面直角坐标系中有一点![]() ,使得
,使得![]() ,请求出点P的坐标;
,请求出点P的坐标;
![]() 点M为直线
点M为直线![]() 上的动点,过点M作y轴的平行线,交
上的动点,过点M作y轴的平行线,交![]() 于点N,点Q为y轴上一动点,且
于点N,点Q为y轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点M的坐标.
为等腰直角三角形,请直接写出满足条件的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空,并在括号内标注理由.
已知:如图①,DE∥BC,∠2=∠B,求证∠B+∠BFE=180°.
证明:∵DE![]() BC(已知),
BC(已知),
∴∠1=∠ ( ).
又∵∠2=∠B( 已知 ),∴∠ =∠ .
∴ EF![]() ( ).
( ).
∴∠B+∠BFE=180°( ).
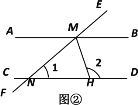
(2)如图②,AB![]() CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.
CD,EF与AB,CD分别相交于点M,N,MH平分∠BMN,与CD相交于点H. 若∠1=40° ,求∠2的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2)
(1)请写出△ABC关于x轴对称的点A1、B1、C1的坐标;
(2)请在这个坐标系中作出△ABC关于y轴对称的△A2B2C2;
(3)计算:△A2B2C2的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(-1,2),C(-1,-2),D(1,-2),点M和点N同时从E(0,2)点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年长江中下游地区发生了特大旱情.为抗旱保丰收,某地政府制定了农户投资购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备投资的金额与政府补的额度存在下表所示的函数对应关系.
(1)分别求y1和y2的函数解析式;
(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com