
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,与y轴交于点
,与y轴交于点![]() ,与x轴交于点C.
,与x轴交于点C.
![]() 求直线
求直线![]() 的函数表达式;
的函数表达式;
![]() 求
求![]() 的面积;
的面积;
![]() 在平面直角坐标系中有一点
在平面直角坐标系中有一点![]() ,使得
,使得![]() ,请求出点P的坐标;
,请求出点P的坐标;
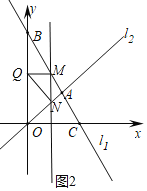
![]() 点M为直线
点M为直线![]() 上的动点,过点M作y轴的平行线,交
上的动点,过点M作y轴的平行线,交![]() 于点N,点Q为y轴上一动点,且
于点N,点Q为y轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点M的坐标.
为等腰直角三角形,请直接写出满足条件的点M的坐标.

【答案】(1)y=-2x+6;(2)3;(3)(5,2)或(5,8);(4)![]() 或
或![]() 或(6,-6) 或(3,0).
或(6,-6) 或(3,0).
【解析】
![]() 先求点A坐标,再用待定系数法求函数解析式.
先求点A坐标,再用待定系数法求函数解析式.
![]() 求点C坐标,以OC为底,点A到x轴距离为高计算.
求点C坐标,以OC为底,点A到x轴距离为高计算.
![]() 观察面积相等两个三角形,有公共边OA,故可看作是以OA为底,高相等
观察面积相等两个三角形,有公共边OA,故可看作是以OA为底,高相等![]() 所以点P在与OA平行的直线上,且到直线OA距离等于点C到OA距离
所以点P在与OA平行的直线上,且到直线OA距离等于点C到OA距离![]() 其中一条即为过点C的直线,根据平移,另一条经过点C关于A的对称点
其中一条即为过点C的直线,根据平移,另一条经过点C关于A的对称点![]() 求出直线后,把
求出直线后,把![]() 代入即求出点P坐标.
代入即求出点P坐标.
![]() 由于直角不确定,需分类讨论,得到MN与M的横坐标的关系
由于直角不确定,需分类讨论,得到MN与M的横坐标的关系![]() 列得方程求解即可.
列得方程求解即可.
解:![]() 点
点![]() 在直线
在直线![]() :
:![]() 上,
上,
![]() ,即
,即![]() ,
,
![]() 直线
直线![]() :
:![]() 过点
过点![]() 、点
、点![]() ,
,
![]() 解得:
解得:![]() ,
,
![]() 直线直线
直线直线![]() 的函数表达式为:
的函数表达式为:![]() ;
;
![]() 令
令![]() ,解得:
,解得:![]() ,
,
![]() 点
点![]() 即
即![]() ,
,
![]() ,
,
![]() ,
,
![]() 当以AO为底边时,两三角形等高,
当以AO为底边时,两三角形等高,
![]() 过点P且与直线AO平行的直线
过点P且与直线AO平行的直线![]() 为:
为:![]() ,
,
![]() 直线
直线![]() 过点
过点![]() ,得
,得![]() 为:
为:![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点
点![]() ,
,
![]() 点
点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,
,
直线![]() 过点
过点![]() ,得
,得![]() 为:
为:![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点
点![]()
综上所述,点P坐标为![]() 或
或![]()
![]() 设
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() 如图1,若
如图1,若![]() ,
,![]() ,
,

则有![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
![]() 或
或![]() ,
,
![]() 如图2,图3,若
如图2,图3,若![]() 或
或![]() ,
,

则![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
![]() 或
或![]()
综上所述,点M的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】工厂工人小李生产A、B两种产品.若生产A产品10件,生产B产品10件,共需时间350分钟;若生产A产品30件,生产B产品20件,共需时间850分钟.
(1)小李每生产一件![]() 种产品和每生产一件
种产品和每生产一件![]() 种产品分别需要多少分钟;
种产品分别需要多少分钟;
(2)小李每天工作8个小时,每月工作25天.如果小李四月份生产![]() 种产品
种产品![]() 件(
件(![]() 为正整数).
为正整数).
①用含![]() 的代数式直接表示小李四月份生产
的代数式直接表示小李四月份生产![]() 种产品的件数;
种产品的件数;
②已知每生产一件![]() 产品可得1.40元,每生产一件
产品可得1.40元,每生产一件![]() 种产品可得2.80元,若小李四月份的工资不少于1500元,求
种产品可得2.80元,若小李四月份的工资不少于1500元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场上的红茶由茶原液与纯净水按一定比例配制而成,其中购买一吨茶原液的钱可以买15 吨纯净水。由于今年以来茶产地连续大旱,茶原液收购价上涨50%.纯净水价也上涨了10%,导致配制的这种茶饮料成本上涨40%,问这种茶饮料中茶原液与纯净水的配制比例为_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段a和射线OA,射线OA上有点B.

(1)用圆规和直尺在射线OA上作线段CD,使点B为CD的中点,点C在点B的左边,且BC=a.(不用写作法,保留作图痕迹)
(2)在(1)的基础上,若OB=12cm,OC=5cm,求线段OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).
(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从全校1200名学生中随机选取一部分学生进行调查,调查情况:A:上网时间 ![]() 小时;B:1小时<上网时间
小时;B:1小时<上网时间 ![]() 小时;C:4小时<上网时间
小时;C:4小时<上网时间 ![]() 小时;D:上网时间>7小时.统计结果制成了如图统计图:
小时;D:上网时间>7小时.统计结果制成了如图统计图:
(1)参加调查的学生有人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在 ![]() 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 ![]() 处飞出(
处飞出( ![]() 在
在 ![]() 轴上),运动员孙可在距
轴上),运动员孙可在距 ![]() 点6米的
点6米的 ![]() 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ![]() ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.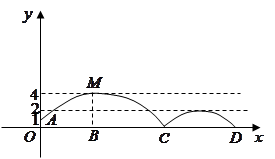
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 ![]() 距守门员多少米?(取
距守门员多少米?(取 ![]() )
)
(3)孙可要抢到足球第二个落地点 ![]() ,他应从第一次落地点
,他应从第一次落地点 ![]() 再向前跑多少米?(取
再向前跑多少米?(取 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.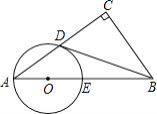
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com