
【题目】已知:如图,直线AB、CD相交于点O,OE⊥OC,OF平分∠AOE.
(1)若![]() ,则∠AOF的度数为______;
,则∠AOF的度数为______;
(2)若![]() ,求∠BOC的度数。
,求∠BOC的度数。

【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据对顶角的性质得到∠AOD=∠BOC=60°,根据垂直的定义得到∠DOE=90°,根据角平分线的定义即可得到结论;
(2)由垂直的定义得到∠DOE=∠COE=90°,根据角平分线的定义得到∠AOE=2∠EOF=180°-2x°,根据对顶角的性质即可得到结论.
∵∠AOD=∠BOC=60°,
∵OE⊥OC于点O,
∴∠DOE=90°,
∴∠AOE=30°,
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=15°,
∠AOE=15°,
故答案为:15°;
(2)∵OE⊥OC于点O,
∴∠COE=∠DOE=90°,
∵∠COF=x°,
∴∠EOF=x°90°,
∵OF平分∠AOE,
∴∠AOE=2∠EOF=2x°180°,
∴∠AOD=90°∠AOE=270°2x°,
∴∠BOC=∠AOD=270°2x°.
故答案为:270°2x°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2 ![]()
B.2 ![]()
C.2 ![]()
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中,放有三个标号分别为1,2,3的质地、大小都相同的小球.任意摸出一个小球,记为x,再从剩余的球中任意摸出一个小球,又记为y,得到点(x,y).
(1)用画树状图或列表等方法求出点(x,y)的所有可能情况;
(2)求点(x,y)在二次函数y=ax2﹣4ax+c(a≠0)图象的对称轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种进价为20 (元/个)的计算器,其销售量y (万个)与销售价格x (元/个)之间为一次函数关系,其变化如下表:
价格x (元/个) | … | 30 | 50 | … |
销售量y (万个) | … | 5 | 3 | … |
同时,销售过程中的其他开支(不含进价)总计40万元.若该公司要获得40万元的净利润,且尽可能让顾客得到实惠,那么销售价格应定为多少?
(注:净利润=总销售额﹣总进价﹣其他开支)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,与y轴交于点
,与y轴交于点![]() ,与x轴交于点C.
,与x轴交于点C.
![]() 求直线
求直线![]() 的函数表达式;
的函数表达式;
![]() 求
求![]() 的面积;
的面积;
![]() 在平面直角坐标系中有一点
在平面直角坐标系中有一点![]() ,使得
,使得![]() ,请求出点P的坐标;
,请求出点P的坐标;
![]() 点M为直线
点M为直线![]() 上的动点,过点M作y轴的平行线,交
上的动点,过点M作y轴的平行线,交![]() 于点N,点Q为y轴上一动点,且
于点N,点Q为y轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点M的坐标.
为等腰直角三角形,请直接写出满足条件的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
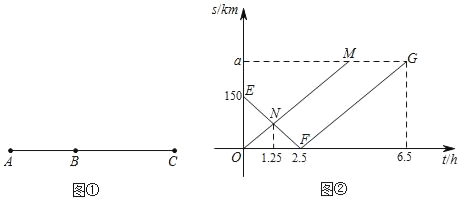
【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年长江中下游地区发生了特大旱情.为抗旱保丰收,某地政府制定了农户投资购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备投资的金额与政府补的额度存在下表所示的函数对应关系.
(1)分别求y1和y2的函数解析式;
(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com