
【题目】2011年长江中下游地区发生了特大旱情.为抗旱保丰收,某地政府制定了农户投资购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备投资的金额与政府补的额度存在下表所示的函数对应关系.
(1)分别求y1和y2的函数解析式;
(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
【答案】
(1)解:设y1=kx,将(5,2)代入得:
2=5k,
解得:k=0.4,
故y1=0.4x,
设y2=ax2+bx,将(2,2.4),(4,3.2)代入得:
![]() ,
,
解得:a=﹣0.2,b=1.6,
∴y2=﹣0.2x2+1.6x;
(2)解:假设投资购买Ⅰ型用x万元、Ⅱ型为(10﹣x)万元,
y=y1+y2=0.4x﹣0.2(10﹣x)2+1.6(10﹣x);
=﹣0.2x2+2.8x﹣4,
当x=﹣ ![]() =7时,y=
=7时,y= ![]() =5.8万元,
=5.8万元,
∴当购买Ⅰ型用7万元、Ⅱ型为3万元时能获得的最大补贴金额,最大补贴金额为5.8万元.
【解析】(1)观察表中的相关数据,将对应的自变量和函数值代入相应的函数解析式,即可求出分别求y1和y2的函数解析式。
(2)抓住已知条件有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元,即y=y1+y2建立函数解析式,求出其顶点坐标,即可求得结论。
【考点精析】利用确定一次函数的表达式和二次函数的最值对题目进行判断即可得到答案,需要熟知确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,0)
B.(6,2)
C.(6,3)
D.(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,OE平分∠AOD,OF⊥OE,OG⊥CD,∠CDO=50°,则下列结论:
① ∠AOE=65°;② OF平分∠BOD;③ ∠GOE=∠DOF;④ ∠AOE=∠GOD,其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.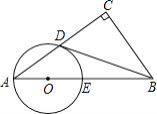
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
辆,一次运完,且恰好每辆车都装满货物. 根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在以下证明中的括号内注明理由:
已知:如图,EF⊥CD于F,GH⊥CD于H.求证:∠1=∠3.

证明:∵EF⊥CD,GH⊥CD(已知),
∴EF∥GH( ).
∴∠1=∠2( ).
∵∠2=∠3( ),
∴∠1=∠3( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于 x 的不等式-3≤x-m<1.5 的整数解之和为 6,那么 m 的取值范围是( )
A.无解B.2<m≤3C.1.5≤m<2.5D.2<m≤2.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com