
【题目】如图,BO,CO分别平分∠ABC和∠ACB

(1)若∠A=60°,求∠BOC;
(2)若∠A=100°,120°,∠BOC又是多少?
【答案】(1)∠BOC=120°;(2)当∠A=100°时∠BOC=140°;当∠A=120°时∠BOC=150°.
【解析】
(1)已知∠A=60°,就可以求出∠ABC与∠ACB的和,从而可以求出∠1与∠4的和,即可求出∠BOC的值;
(2)利用(1)中的方法分别计算∠A=100°和∠A=120°时∠BOC的值即可.
解:∵BO、CO分别平分∠ABC和∠ACB,
∴∠1=∠2,∠3=∠4,
∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
即∠1+∠2+∠3+∠4=120°,
∴∠1+∠4=60°,
∴∠BOC=180°-60°=120°;
(2)若∠A=100°,
则∠1+∠2+∠3+∠4=180°-100°=80°,
∴∠1+∠4=40°,
∴∠BOC=180°-40°=140°.
若∠A=120°,
∴∠1+∠2+∠3+∠4=180°-120°=60°,
∴∠1+∠4=30°,
∴∠BOC=180°-30°=150°.


科目:初中数学 来源: 题型:
【题目】如图,已知线段a和射线OA,射线OA上有点B.

(1)用圆规和直尺在射线OA上作线段CD,使点B为CD的中点,点C在点B的左边,且BC=a.(不用写作法,保留作图痕迹)
(2)在(1)的基础上,若OB=12cm,OC=5cm,求线段OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从全校1200名学生中随机选取一部分学生进行调查,调查情况:A:上网时间 ![]() 小时;B:1小时<上网时间
小时;B:1小时<上网时间 ![]() 小时;C:4小时<上网时间
小时;C:4小时<上网时间 ![]() 小时;D:上网时间>7小时.统计结果制成了如图统计图:
小时;D:上网时间>7小时.统计结果制成了如图统计图:
(1)参加调查的学生有人;
(2)请将条形统计图补全;
(3)请估计全校上网不超过7小时的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() (
( ![]() 是常数).
是常数).
(1)求证:不论 ![]() 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿 ![]() 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与 ![]() 轴只有一个公共点?
轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在 ![]() 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 ![]() 处飞出(
处飞出( ![]() 在
在 ![]() 轴上),运动员孙可在距
轴上),运动员孙可在距 ![]() 点6米的
点6米的 ![]() 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ![]() ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.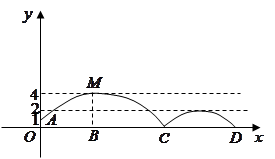
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 ![]() 距守门员多少米?(取
距守门员多少米?(取 ![]() )
)
(3)孙可要抢到足球第二个落地点 ![]() ,他应从第一次落地点
,他应从第一次落地点 ![]() 再向前跑多少米?(取
再向前跑多少米?(取 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A.(4,0)
B.(6,2)
C.(6,3)
D.(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在以下证明中的括号内注明理由:
已知:如图,EF⊥CD于F,GH⊥CD于H.求证:∠1=∠3.

证明:∵EF⊥CD,GH⊥CD(已知),
∴EF∥GH( ).
∴∠1=∠2( ).
∵∠2=∠3( ),
∴∠1=∠3( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com