
【题目】如图,已知四边形ABCD的顶点为A(1,2),B(-1,2),C(-1,-2),D(1,-2),点M和点N同时从E(0,2)点出发,沿四边形的边做环绕匀速运动,M点以1单位/s的速度做逆时针运动,N点以2单位/s的速度做顺时针运动,则点M和点N第2017次相遇时的坐标为_____.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图①,ABCD是边长为60cm的正方形硬纸片,切去四个全等的等腰直角三角形(阴影部分所示),其中E,F在AB上;再沿虚线折起,点A,B,C,D恰好重合于点O处(如图②所示),形成有一个底面为正方形GHMN的包装盒,设AE=x (cm).
(1)求线段GF的长;(用含x的代数式表示)
(2)当x为何值时,矩形GHPF的面积S (cm2)最大?最大面积为多少?
(3)试问:此种包装盒能否放下一个底面半径为15cm,高为10cm的圆柱形工艺品,且使得圆柱形工艺品的一个底面恰好落在图②中的正方形GHMN内?若能,请求出满足条件的x的值或范围;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全校学生对新闻,体育.动画、娱乐、戏曲五类电视节目的喜爱情况,机调查了100名学生,结果如扇形图所示,依据图中信息,回答下列问题: (1)在被调查的学生中,喜欢“动画”节目的学生有 _____(名); (2)在扇形统计图中,喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 _____(度).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )
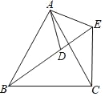
A. ∠ABD=∠ACE B. BD=CE C. ∠BAD=∠CAE D. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.

(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=30°,求∠MGN+∠MPN的度数;
(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.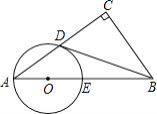
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连结OA,二次函数y=x2图象从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
(1)求线段OA所在直线的函数解析式;
(2)设二次函数顶点M的横坐标为m,当m为何值时,线段PB最短,并求出二次函数的表达式;
(3)当线段PB最短时,二次函数的图象是否过点Q(a,a﹣1),并说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新个税法于2018年9月1日全面实施,工资、薪金所得基本减除费用标准由3500元提高至5000元,并按新的税率表计算纳税:
序号 | 税前每月工资的各部分 | 税率 |
1 | 不超过5000元部分 | 0% |
2 | 超过5000元至8000元的部分 | 3% |
3 | 超过8000元至17000元的部分 | 10% |
4 | 超过17000元至30000元的部分 | 20% |
5 | 超过30000元至40000元的部分 | 25% |
6 | 超过40000元至60000元的部分 | 30% |
7 | 超过60000元至80000元的部分 | 35% |
8 | 超过80000元的部分 | 45% |
(1)在新个税法实施后,小王没扣税前某月工资7800元,他这个月应交税 元;
(2)在新个税法实施后,若小李没扣税前某月工资x元![]() ,他这个月交税y元,则y= ;
,他这个月交税y元,则y= ;
(3)在新个税法实施后,一企业某月把奖金放在工资里发放(奖金跟工资一起扣税),该企业员工小刘这个月领取了工资加奖金(税后)26410元.已知小刘没扣税前工资为a元![]() ,若工资和奖金分两次发放(资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
,若工资和奖金分两次发放(资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com