
【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.

【答案】(1)y=x2﹣4x+3;(2)![]() ;(3)点P(1,0)或(2,﹣1);(4)M(2,﹣3).
;(3)点P(1,0)或(2,﹣1);(4)M(2,﹣3).
【解析】试题分析:(1)把点A、B的坐标代入抛物线解析式,解方程组得到b、c的值,即可得解;
(2)求出点C的坐标,再利用待定系数法求出直线AC的解析式,再根据抛物线解析式设出点P的坐标,然后表示出PD的长度,再根据二次函数的最值问题解答;
(3)①∠APD是直角时,点P与点B重合,②求出抛物线顶点坐标,然后判断出点P为在抛物线顶点时,∠PAD是直角,分别写出点P的坐标即可;
(4)根据抛物线的对称性可知MA=MB,再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时,|MA﹣MC|最大,然后利用待定系数法求出直线BC的解析式,再求解即可.
试题解析:解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),∴![]() ,解得
,解得![]() ,∴抛物线解析式为y=x2﹣4x+3;
,∴抛物线解析式为y=x2﹣4x+3;
(2)令x=0,则y=3,∴点C(0,3),则直线AC的解析式为y=﹣x+3,设点P(x,x2﹣4x+3).∵PD∥y轴,∴点D(x,﹣x+3),∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣![]() )2+
)2+![]() .∵a=﹣1<0,∴当x=
.∵a=﹣1<0,∴当x=![]() 时,线段PD的长度有最大值
时,线段PD的长度有最大值![]() ;
;
(3)①∠APD是直角时,点P与点B重合,此时,点P(1,0),②∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1).∵A(3,0),∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,此时,点P(2,﹣1).
综上所述:点P(1,0)或(2,﹣1)时,△APD能构成直角三角形;
(4)由抛物线的对称性,对称轴垂直平分AB,∴MA=MB,由三角形的三边关系,|MA﹣MC|<BC,∴当M、B、C三点共线时,|MA﹣MC|最大,为BC的长度,设直线BC的解析式为y=kx+b(k≠0),则![]() ,解得:
,解得: ![]() ,∴直线BC的解析式为y=﹣3x+3.∵抛物线y=x2﹣4x+3的对称轴为直线x=2,∴当x=2时,y=﹣3×2+3=﹣3,∴点M(2,﹣3),即,抛物线对称轴上存在点M(2,﹣3),使|MA﹣MC|最大.
,∴直线BC的解析式为y=﹣3x+3.∵抛物线y=x2﹣4x+3的对称轴为直线x=2,∴当x=2时,y=﹣3×2+3=﹣3,∴点M(2,﹣3),即,抛物线对称轴上存在点M(2,﹣3),使|MA﹣MC|最大.



 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
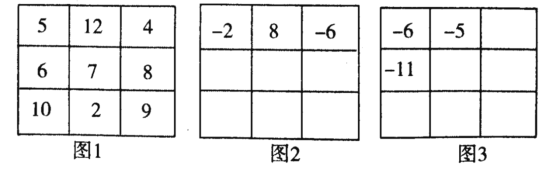
【题目】将九个数填在3×3(3行3列)的方格中,如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等,这样的图称为“广义的三阶幻方”,如图1就是一个满足条件的广义三阶幻方.图2、图3的广义三阶幻方中分别给出了三个数.请直接将图2、图3的其余6个数全填上;
(提示:三阶幻方的幻和=中心数字×3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C=90°,∠BAC=30°,点D为边BC上的点,连接AD,∠BAD=α,点D关于AB的对称点为E,点E关于AC的对称点为G,线段EG交AB于点F,连接AE,DE,DG,AG.
(1)依题意补全图形;
(2)求∠AGE的度数(用含α的式子表示);
(3)用等式表示线段EG与EF,AF之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价400元,领带每条定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案:
方案①:买一套西装送一条领带;
方案②:西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20)
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);
若该客户按方案②购买,需付款 元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法并计算出此种方案的付款金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列火车匀速行驶,经过一条长475m的A隧道用了32s的时间.A隧道顶上有一盏灯,垂直向下发光,行驶过程中灯光照在火车上的时间是13s
(1)求这列火车的长度;
(2)若这列火车经过A隧道侯按原速度又经过了一条长750m的B隧道,求这列火车经过B隧道需要的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
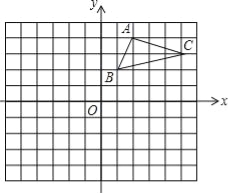
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
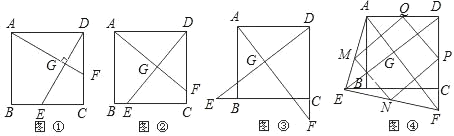
【题目】如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com