
����Ŀ��ij��װ������һ����װ���������װÿ����400Ԫ�����ÿ������50Ԫ�������ڿ�չ������ڼ䣬��ͻ��ṩ�����Żݷ�����
�����٣���һ����װ��һ�������
�����ڣ���װ������������۵�90%���
��ij�ͻ�Ҫ���÷�װ��������װ20�ף����x����x��20��
��1�����ÿͻ��������ٹ����踶������ Ԫ���ú�x�Ĵ���ʽ��ʾ����
���ÿͻ��������ڹ����踶������ Ԫ���ú�x�Ĵ���ʽ��ʾ����
��2����x=30��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��3���������Żݷ�����ͬʱʹ�ã���x=30ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�������������ַ����ĸ����
���𰸡���1�� ![]() ��
��![]() ����2���������ٹ����Ϊ���㣬����������3�����ԣ����ɼ�����
����2���������ٹ����Ϊ���㣬����������3�����ԣ����ɼ�����
��������
��1����������ֱ��г�����ʽ����������
��2����x=30���루1������������ʽ���������ý��ۣ�
��3��ץסʡǮ�뷽�������ַ�����ѡ�ã�
��1���������ٹ����踶�400��20+��x-20����50
=![]() Ԫ��
Ԫ��
�������ڹ����踶�400��90%��20+50��90%��x
=![]() ��Ԫ��
��Ԫ��
��2����![]() ʱ
ʱ
�����٣�![]()
�����ڣ�![]()
![]()
![]()
�𣺴�ʱ�������ٹ����Ϊ����.
��3���÷�������20����װ��20����������÷�������10�����.
�ܼ�ǮΪ![]()
![]()
���Կ���


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ܵ��ڳ����ѻ����ռ�����������ʡ�����ؼ���ũ������ƹ㣬Ϊ��Ӧ���٣�ij�̳��ƻ���3800Ԫ�������ܵ�120ֻ�������ֽ��ܵƵĽ��ۡ��ۼ����±���

��1����ס������ֽ��ܵƸ�������ֻ��
��2��ȫ������120ֻ���ܵƺ��̳����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
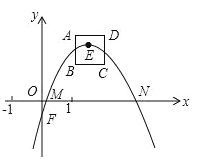
����Ŀ����ͼ��������l��y=��x2+bx+c��b��cΪ���������䶥��E��������ABCD�ڻ��������֪��A��1��2����B��1��1����C��2��1����
��1��ֱ��д����D������_____________��
��2����l������B��C����l�Ľ���ʽ��
��3����l��x�ύ�ڵ�M��N����l�Ķ���E���D�غ�ʱ�����߶�MN��ֵ��������E��������ABCD�ڻ����ʱ��ֱ��д���߶�MN��ȡֵ��Χ��
��4����l����������ABCD������������ֱ��д�����з���������c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
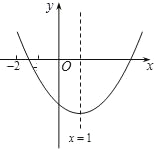
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ�����н��ۣ�
��1��c��0��
��2��b��0��
��3��4a+2b+c��0��
��4����a+c��2��b2��
���в���ȷ���У�������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�������и���������Ӧ�ļ����
������2.5��������1��2����|��2|����22��0�� ![]() ����1.5��
����1.5��
��������{�� �� ��}
��������{�� �� ��}
��2���ѱ�ʾ��������ĵ㻭�������ϣ��ٰ���С�����˳�����������Ű���Щ������������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������ÿ��С�����α߳�����1��С�����εĶ����Ϊ��㣬�������������зֱ�����ͼ�Σ�
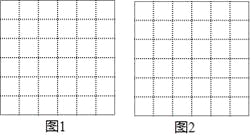
![]() �������л�����Ϊ
�������л�����Ϊ![]() ���߶�AB.
���߶�AB.
![]() �������л���һ������Ϊ
�������л���һ������Ϊ![]() �����Ϊ3�ĵ���
�����Ϊ3�ĵ���![]() DEF��
DEF��
(3)��������������߳��ֱ�Ϊ![]() ��
��![]() ��
��![]() �����������Ϊ__________
�����������Ϊ__________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��������y=x2+bx+c����A��3��0����B��1��0������y���ڵ�C����P�Ǹ���������һ���㣬��P��C������������A���˶�����P�����A�غϣ�������P��PD��y�ύֱ��AC�ڵ�D��
��1���������ߵĽ���ʽ��
��2�����P���˶��Ĺ������߶�PD���ȵ����ֵ��
��3����APD�ܷ�ֱ�������Σ�������ֱ��д����P���꣬��������˵�����ɣ�
��4���������߶Գ������Ƿ���ڵ�Mʹ|MA��MC|����������������M�����꣬����������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����ĵ���ͼ����Ӧ�ĵ�ʽ��̽�����еĹ��ɣ�
��1������۲죬���ڢܺ���ĺ�����д����Ӧ�ĵ�ʽ��
![]()
��1=1 ��1+2=![]() =3 ��1+2+3=
=3 ��1+2+3=![]() =6 ���� ����
=6 ���� ����
��2����ϣ�1���۲����е���ͼ�����ڢݺ���ĺ�����д����Ӧ�ĵ�ʽ��
![]()
1=12��1+3=22��3+6=32��6+10=42���� ����
��3��ͨ�����룬д����2�������n���������Ӧ�ĵ�ʽ�� ����
���𰸡���1��10����2������������3��![]()
�������������������1�����ݢ٢ڢ۹۲�ᷢ�ֵ��ĸ�ʽ�ӵĵȺŵ������1+2+3+4���ұ߷������ǣ�1+4����4���Ӷ��õ����ɣ�
��2��ͨ���۲췢�������10+15���ұ���25��5��ƽ����
��3������һЩ����ʽ�ӽ������������Ρ��۲졢�Ƚϣ����ɳ�һ����ɣ�
�����������1�����������������Ĺ��ɿ�֪��1+2+3+4��![]() ��10��
��10��
��2����ͼʾ��֪���������5��5=25������10+15=52��
��3���ɣ�1����2����֪![]()
�㾦����Ҫ������ѧ��ͨ�����������Ӷ������ܽ��һ����۵������������ҹ��ɵ���Ŀ����Ӧ�ҳ���Щ���ַ����˱仯���ǰ���ʲô���ɱ仯�ģ�ͨ�������ҵ������ֵı仯���ɺ���һ��ͳһ��ʽ�ӱ�ʾ���仯�����Ǵ�����Ŀ�е��ѵ㣮
�����͡������
��������
19
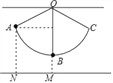
����Ŀ����ͼ����ϸ������һ��С��С������ֱƽ���ڵ�A��C��������ذڶ���A����������AN=14cm��С������͵�Bʱ����������BM=5cm����AOB=66������ϸ��OB�ij��ȣ����ο����ݣ�sin66���0.91��cos66���0.40��tan66���2.25��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������48�ֵĴ��ͻ����������Ļ����dz�14m����2.5m����3m�ij����壬���м��ֻ���18�֣����ֻ���70m3�������ֻ���ÿ�ֵ����Ϊ2.5m3�����ֻ���ÿ������0.5�֣��ʣ�
��1���ס������ֻ����Ƿ���װ�ϳ�����˵�����ɣ�
��2��Ϊ���������ó����������ͻ�����ݻ������ֻ���Ӧ��װ���ٶ֣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com