
【题目】一辆最大载重48吨的大型货车,货车的货箱是长14m,宽2.5m,高3m的长方体,现有甲种货物18吨,乙种货物70m3,而甲种货物每吨的体积为2.5m3,乙种货物每立方米0.5吨.问:
(1)甲、乙两种货物是否都能装上车?请说明理由.
(2)为了最大地利用车的载重量和货箱的容积,两种货物应各装多少吨?
【答案】(1)不能全部装上船,见解析;(2)装甲种货物为18吨,装乙种货物为30吨
【解析】
(1)根据货物的总重量与货车的总载重进行比较,得到答案.
(2)通过理解题意可知本题存在两个等量关系,即甲种货物的总质量+乙种货物的总质量=48吨,甲种货物所占的总体积+乙种货物所占的总体积=货箱体积,根据这两个等量关系设出未知数,列出方程求解即可.
解:(1)由于18+![]() =158>48,故不能全部装上船.
=158>48,故不能全部装上船.
(2)设装甲种货物质量为x吨,装乙种货物质量为(48﹣x)吨.
根据题意,得2.5x+![]() =14×2.5×3,
=14×2.5×3,
解得x=18.
则48﹣x=48﹣18=30(吨)
答:装甲种货物为18吨,装乙种货物为30吨


科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价400元,领带每条定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案:
方案①:买一套西装送一条领带;
方案②:西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20)
(1)若该客户按方案①购买,需付款 元(用含x的代数式表示);
若该客户按方案②购买,需付款 元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法并计算出此种方案的付款金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
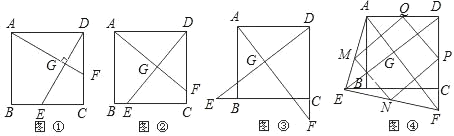
【题目】如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
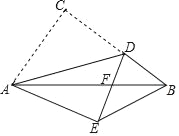
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
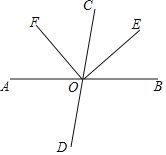
【题目】如图,直线AB,CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF⊥OE.
(1)求∠COF的度数;
(2)说明OF平分∠AOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
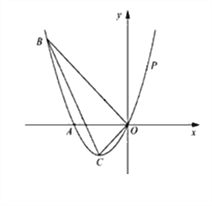
【题目】如图,已知抛物线经过A(-2,0)B(-3,3)及原点O,顶点为C。
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标。
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥ x轴,垂足为M,是否存在点P点使得以P、M、A为顶点的三角形与△BOC相似?若存在,求P点的坐标,若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
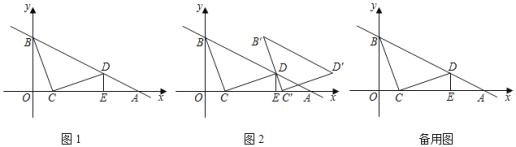
【题目】如图1,在平面直角坐标系中,直线y=-![]() x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com