
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.甲、乙两种树苗的成活率分别为85%,90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗的数量应满足怎样的条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,
, ![]() 在数轴上对应的实数分别是
在数轴上对应的实数分别是![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() 满足
满足![]() .
.
(![]() )求线段
)求线段![]() 的长.
的长.
(![]() )点
)点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,且
,且![]() 是方程
是方程![]() 的解,在数轴上是否存在点
的解,在数轴上是否存在点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 对应的数;若不存在,说明理由.
对应的数;若不存在,说明理由.
(![]() )在(
)在(![]() )和(
)和(![]() )的条件下,点
)的条件下,点![]() ,
, ![]() ,
, ![]() 同时开始在数轴上运动,若点
同时开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度是速度向左运动,点
个单位长度是速度向左运动,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,点
个单位长度的速度向右运动,点![]() 与点
与点![]() 之间距离表示为
之间距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .设运动时间为
.设运动时间为![]() 秒,试探究,随着时间
秒,试探究,随着时间![]() 的变化,
的变化, ![]() 与
与![]() 满足怎样的数量关系?请写出相应的等式.
满足怎样的数量关系?请写出相应的等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB:y=﹣ ![]() x+5与x轴、y轴分别交于点A、B,y轴上点C的坐标为(0,10).
x+5与x轴、y轴分别交于点A、B,y轴上点C的坐标为(0,10).
(1)求A、B两点的坐标;
(2)动点M从A点出发,以每秒1个单位长度的速度,沿x轴向左运动,连接CM.设点M的运动时间为t,△COM的面积为S,求S与t的函数关系式;(并标出自变量的取值范围)
(3)直线AB与直线CM相交于点N,点P为y轴上一点,且始终保持PM+PN最短,当t为何值时,△COM≌△AOB,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的结论有 . 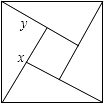
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列运算 ①由( ![]() )(
)( ![]() )=1,得
)=1,得 ![]() =
= ![]() ;
;
②由( ![]() )(
)( ![]() )=1,得
)=1,得 ![]() =
= ![]() ;
;
③由( ![]()
![]() )(
)( ![]()
![]() )=1,得
)=1,得 ![]() =
= ![]()
![]() ;
;
④由( ![]()
![]() )(
)( ![]()
![]() )=1,得
)=1,得 ![]() =
= ![]()
![]() ;
;
…
(1)通过观察,将你发现的规律用含有n的式子表示出来.
(2)利用你发现的规律,计算: ![]()
![]()
![]()
![]() +…+
+…+ ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com