
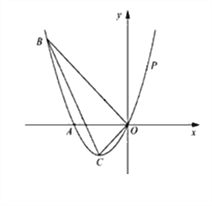
【题目】如图,已知抛物线经过A(-2,0)B(-3,3)及原点O,顶点为C。
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标。
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥ x轴,垂足为M,是否存在点P点使得以P、M、A为顶点的三角形与△BOC相似?若存在,求P点的坐标,若不存在,说明理由。
【答案】(1)y=x2+x(2)D1(1,3),D2(-3,3),C(-1,-1)(3)(![]() ,
,![]() )或(3,15)
)或(3,15)
【解析】试题分析:本题着重考查了待定系数法求二次函数解析式、平行四边形的性质、相似三角形的判定和性质等知识点,综合性强,同时也考查了学生分类讨论,数形结合的数学思想方法.
(1)设抛物线的解析式为y=ax2+bx+c(a≠0),把点A(-2,0),B(-3,3),O(0,0),代入求出a,b,c的值即可;
(2)首先由A的坐标可求出OA的长,再根据四边形AODE是平行四边形,D在对称轴直线x=-1右侧,进而可求出D横坐标为:-1+2=1,代入抛物线解析式即可求出其横坐标;
(3)分△PMA∽△COB和△PMA∽△BOC表示出PM和AM,从而表示出点P的坐标,代入求得的抛物线的解析式即可求得t的值,从而确定点P的坐标.
试题解析:(1)抛物线的解析式为![]() ;
;
(2)①当AE为边时,
∵A、O、D、E为顶点的四边形是平行四边形,
∴DE=AO=2,则D在x轴下方不可能,
∴D在轴上方且DE=2,则D1(1,3),D2(﹣3,3),
②当AO为对角线时,则DE与AO互相平分,
∵点E在对称轴上,且线段AO的中点横坐标为-1,
由对称性知,符合条件的点D只有一个,与点C重合,即C(-1,-1),
故符合条件的点D有三个,分别是D1(1,3),D2(-3,3),C(-1,-1)。
(3)存在,如图:
∵B(-3,3),C(-1,-1),
根据勾股定理得:
BO2=18,CO2=2,BC2=20,
∴BO2+CO2=BC2,
∴△BOC是直角三角形,
假设存在点P,使以P,M,A为顶点的 三角形与△BOC相似,
设P(x,y),
由题意知x>0,y>0,且![]() ,
,
①若△AMP∽△BOC,
则![]() ,即x+2=3(x2+2x)得:
,即x+2=3(x2+2x)得:![]() ,x2=-2(舍去)当
,x2=-2(舍去)当![]() 时,
时,![]() ,即P(
,即P(![]() );
);
②若△PMA∽△BOC,![]() ,
,
即:x2+2x=3(x+2),
得:x1=3,x2=-2(舍去),
当x=3时,y=15,即P(3,15),
故符合条件的点P有两个,分别是P(![]() )或(3,15).
)或(3,15).


科目:初中数学 来源: 题型:
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
【答案】(1)10;(2)见解析;(3)![]()
【解析】试题分析:(1)根据①②③观察会发现第四个式子的等号的左边是1+2+3+4,右边分子上是(1+4)×4,从而得到规律;
(2)通过观察发现左边是10+15,右边是25即5的平方;
(3)过对一些特殊式子进行整理、变形、观察、比较,归纳出一般规律.
试题解析:(1)根据题中所给出的规律可知:1+2+3+4=![]() =10;
=10;
(2)由图示可知点的总数是5×5=25,所以10+15=52.
(3)由(1)(2)可知![]()
点睛:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
【题型】解答题
【结束】
19
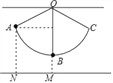
【题目】如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆最大载重48吨的大型货车,货车的货箱是长14m,宽2.5m,高3m的长方体,现有甲种货物18吨,乙种货物70m3,而甲种货物每吨的体积为2.5m3,乙种货物每立方米0.5吨.问:
(1)甲、乙两种货物是否都能装上车?请说明理由.
(2)为了最大地利用车的载重量和货箱的容积,两种货物应各装多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同。
(1)从中任意抽取一张卡片,则该卡片上写有数字1的概率是;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率。(请利用树状图或列表法说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝“春节”,市政府决定在市政广场上增一排灯花,其设计由以下图案逐步演变而成,其中圆圈代表灯花中的灯泡,n代表第n次演变过程,s代表第n次演变后的灯泡的个数,仔细观察下列演变过程,当n=7时,s=( ).
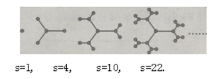
A.162B.176C.190D.214
查看答案和解析>>
科目:初中数学 来源: 题型:
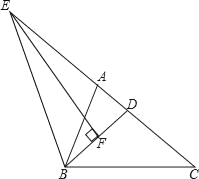
【题目】在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于点E.
(1)求证:ED2=EAEC;
(2)若ED=6,BD=CD=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com