
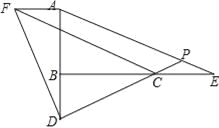
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.

【答案】(1)△CDF是等腰三角形;(2)∠APD=45°.
【解析】试题分析:(1)利用SAS证明△AFD和△BDC全等,再利用全等三角形的性质得出FD=DC,即可判断三角形的形状;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,利用SAS证明△AFD和△BDC全等,再利用全等三角形的性质得出FD=DC,∠FDC=90°,即可得出∠FCD=∠APD=45°.
试题解析:(1)△CDF是等腰直角三角形,理由如下:
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,
在△FAD与△DBC中, 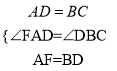 ,∴△FAD≌△DBC(SAS),
,∴△FAD≌△DBC(SAS),
∴FD=DC,∴△CDF是等腰三角形,∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,如图,∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,在△FAD与△DBC中, 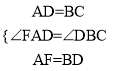 ,∴△FAD≌△DBC(SAS),
,∴△FAD≌△DBC(SAS),
∴FD=DC,∴△CDF是等腰三角形,∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,∴△CDF是等腰直角三角形,
∴∠FCD=45°,∵AF∥CE,且AF=CE,∴四边形AFCE是平行四边形,
∴AE∥CF,∴∠APD=∠FCD=45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
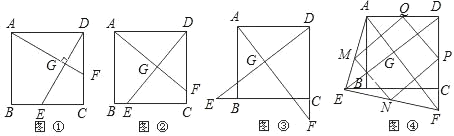
【题目】如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
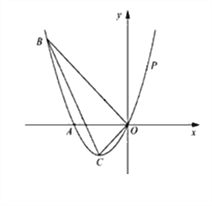
【题目】如图,已知抛物线经过A(-2,0)B(-3,3)及原点O,顶点为C。
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标。
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥ x轴,垂足为M,是否存在点P点使得以P、M、A为顶点的三角形与△BOC相似?若存在,求P点的坐标,若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝“春节”,市政府决定在市政广场上增一排灯花,其设计由以下图案逐步演变而成,其中圆圈代表灯花中的灯泡,n代表第n次演变过程,s代表第n次演变后的灯泡的个数,仔细观察下列演变过程,当n=7时,s=( ).
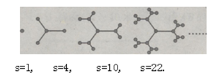
A.162B.176C.190D.214
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
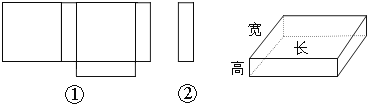
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活中处处有数学,下列原理运用错误的是![]()
![]() .
.
A.建筑工人砌墙时拉的参照线是运用“两点之间线段最短”的原理
B.修理损坏的椅子腿时斜钉的木条是运用“三角形稳定性”的原理
C.测量跳远的成绩是运用“垂线段最短”的原理
D.将车轮设计为圆形是运用了“圆的旋转对称性”原理
查看答案和解析>>
科目:初中数学 来源: 题型:
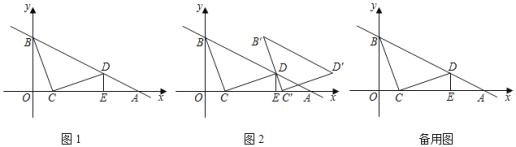
【题目】如图1,在平面直角坐标系中,直线y=-![]() x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com