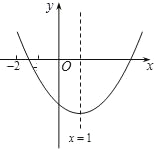
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图，下列结论：
（1）c＜0；
（2）b＞0；
（3）4a+2b+c＞0；
（4）（a+c）2＜b2．
其中不正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线
与x轴交于点A（1，0）和B（4，0）．
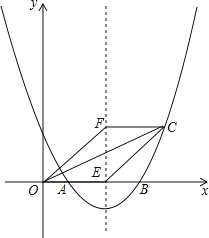
（1）求抛物线的解析式；
（2）若抛物线的对称轴交x轴于点E，点F是位于x轴上方对称轴上一点，FC∥x轴，与对称轴右侧的抛物线交于点C，且四边形OECF是平行四边形，求点C的坐标；
（3）在（2）的条件下，抛物线的对称轴上是否存在点P，使△OCP是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
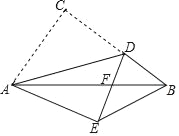
【题目】如图，已知Rt△ABC中，∠C=90°，∠BAC=30°，点D为边BC上的点，连接AD，∠BAD=α，点D关于AB的对称点为E，点E关于AC的对称点为G，线段EG交AB于点F，连接AE，DE，DG，AG.
（1）依题意补全图形；
（2）求∠AGE的度数（用含α的式子表示）；
（3）用等式表示线段EG与EF，AF之间的数量关系，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知数轴上点A表示的数为﹣7，点B表示的数为5，点C到点A，点B的距离相等，动点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动的时间为t（t＞0）秒．
（1）点C表示的数是 ；
（2）求当t等于多少秒时，点P到达点B处；
（3）点P表示的数是 （用含有t的代数式表示）；
（4）求当t等于多少秒时，PC之间的距离为2个单位长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某服装厂生产一种西装和领带，西装每套定价400元，领带每条定价50元．厂方在开展促销活动期间，向客户提供两种优惠方案：
方案①：买一套西装送一条领带；
方案②：西装和领带都按定价的90%付款．
现某客户要到该服装厂购买西装20套，领带x条（x＞20）
（1）若该客户按方案①购买，需付款 元（用含x的代数式表示）；
若该客户按方案②购买，需付款 元（用含x的代数式表示）；
（2）若x=30，通过计算说明此时按哪种方案购买较为合算？
（3）若两种优惠方案可同时使用，当x=30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法并计算出此种方案的付款金额．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察算式：1×3+1＝4＝22；2×4+1＝9＝32；3×5+1＝16＝42；4×6+1＝25＝52，…
（1）请根据你发现的规律填空：6×8+1＝（ ）2；
（2）用含n的等式表示上面的规律： ；
（3）用找到的规律解决下面的问题：
计算：（1+
）（1+
）（1+
）（1+
）…（1+
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点E处，连接DE交AB于点F，当△DEB是直角三角形时，DF的长为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
