
【题目】如图,![]() 为
为![]() 的切线,
的切线,![]() 为切点,直线
为切点,直线![]() 交
交![]() 于点
于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() .
.
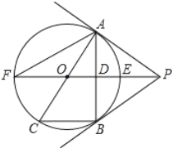
(1)求证:直线![]() 为
为![]() 的切线;
的切线;
(2)试探究线段![]() 、
、![]() 、
、![]() 之间的等量关系,并加以证明;
之间的等量关系,并加以证明;
(3)若![]() ,
,![]() ,求
,求![]() 的值和线段
的值和线段![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接OB,根据垂径定理的知识,得出OA=OB,∠POA=∠POB,继而证明△PAO≌△PBO,然后利用全等三角形的性质结合切线的判定定理即可得出结论.
(2)先证明△OAD∽△OPA,利用相似三角形的性质得出OA与OD、OP的关系,然后将EF=20A代入关系式即可.
(3)根据题意可确定OD是△ABC的中位线,设AD=x,然后利用三角函数的知识表示出FD、OA,在Rt△AOD中,利用勾股定理解出x的值,继而能求出cos∠ACB,再由(2)可得OA2=ODOP,代入数据即可得出PE的长.
(1)连接OB,
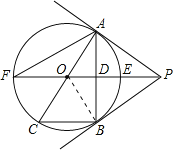
∵PB是⊙O的切线,
∴∠PBO=90°,
∵OA=OB,BA⊥PO于D,
∴AD=BD,∠POA=∠POB,
又∵PO=PO,
∴△PAO≌△PBO(SAS),
∴∠PAO=∠PBO=90°,
∴OA⊥PA,
∴直线PA为⊙O的切线.
(2)EF2=4ODOP.
证明:∵∠PAO=∠PDA=90°
∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°,
∴∠OAD=∠OPA,
∴△OAD∽△OPA,
∴![]() ,即OA2=ODOP,
,即OA2=ODOP,
又∵EF=2OA,
∴EF2=4ODOP.
(3)∵OA=OC,AD=BD,BC=6,
∴OD=![]() BC=3(三角形中位线定理),
BC=3(三角形中位线定理),
设AD=x,
∵tan∠F=![]() ,
,
∴FD=2x,OA=OF=2x-3,
在Rt△AOD中,由勾股定理,得(2x-3)2=x2+32,
解之得,x1=4,x2=0(不合题意,舍去),
∴AD=4,OA=2x-3=5,
∵AC是⊙O直径,
∴∠ABC=90°,
又∵AC=2OA=10,BC=6,
∴cos∠ACB=![]() .
.
∵OA2=ODOP,
∴3(PE+5)=25,
∴PE=![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
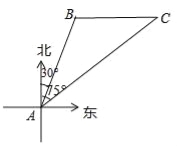
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
![]()
![]() (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
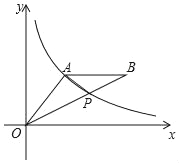
【题目】如图,A(3,m)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y=![]() 的图象于点P(2
的图象于点P(2![]() ,
,![]() ).
).
(1)求m的值和点B的坐标;
(2)连接AP,求△OAP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
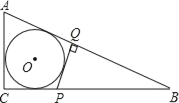
【题目】如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工材料经销公司购进一种化工原料若干千克,物价部门规定其销售单价不低于进价,不高于60元/千克,经市场调查发现:销售单价定为60元/千克时,每日销售20千克;如调整价格,每降价1元/千克,每日可多销售2千克.
(1)已知某天售出该化工原料40千克,则当天的销售单价为 元/千克;
(2)该公司现有员工2名,每天支付员工的工资为每人每天90元,每天应支付其他费用108元,当某天的销售价为46元/千克时,收支恰好平衡.
①求这种化工原料的进价;
②若公司每天的纯利润(收入﹣支出)全部用来偿还一笔10000元的借款,则至少需多少天才能还清借款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=2![]() ,则顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的面积是_____.
,则顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=3.
(1)试在AB上确定点D的位置,△ACD∽△ABC;
(2)试在AC的延长线上确定点E的位置,使△AEB∽△ABC,此时BE与DC有怎样的位置关系?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
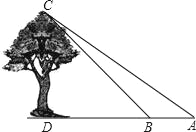
【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为35°;(2)在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;(3)量出A,B两点间的距离为4.5米.请你根据以上数据求出大树CD的高度.(精确到0.1米)(可能用到的参考数据sin35°≈0.57cos35°≈0.82,tan35°≈0.70)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com