
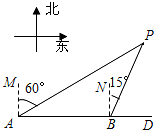
 一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向上.
一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向上.分析 (1)过点B作BC⊥AP于点C,先求出BC、AC的长度,然后确定∠CBP的度数,从而得出CB=PC,再根据AP=AC+PC即可得出答案;
(2)过点P作PD⊥AB于点D,根据AD=APcos30°和BD=AD-AB,求出AC和BD,再根据速度=$\frac{路程}{时间}$,即可得出答案.
解答 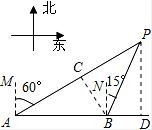 解:(1)过点B作BC⊥AP于点C,在Rt△ABC中,
解:(1)过点B作BC⊥AP于点C,在Rt△ABC中,
∵∠ACB=90°,∠BCA=30°,
∴BC=ABsin30°=20,
∴AC=ABcos30°=20$\sqrt{3}$,
∵∠PBD=75°,∠ABC=60°,
∴∠CBP=45°,
∴CB=PC,
∴AP=AC+PC=(20+20$\sqrt{3}$)海里;
(2)过点P作PD⊥AB于点D,
则AD=APcos30°=(20+20$\sqrt{3}$)×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$+30,
∴BD=AD-AB=10$\sqrt{3}$+30-40=10$\sqrt{3}$-10,
∴轮船每小时航行(10$\sqrt{3}$-10)÷$\frac{1}{4}$=(40$\sqrt{3}$-40)海里;
答:轮船每小时航行(40$\sqrt{3}$-40)海里.
点评 本题考查解直角三角形的应用,有一定的难度,注意在解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11.8×103 | B. | 1.2×104 | C. | 1.18×104 | D. | 1.2×103 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com