
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
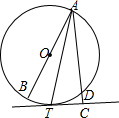 如图,AB是⊙O的直径,D是⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C
如图,AB是⊙O的直径,D是⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C查看答案和解析>>
科目:初中数学 来源: 题型:选择题
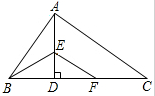 如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )
如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )| A. | ①③ | B. | ①⑤ | C. | ③④ | D. | ①②⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
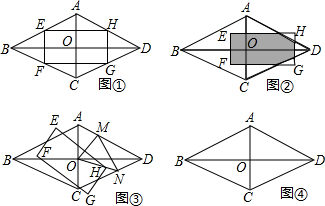
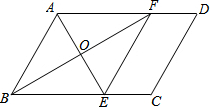 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
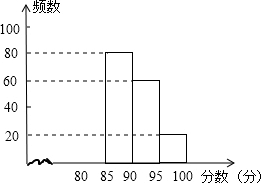 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com