
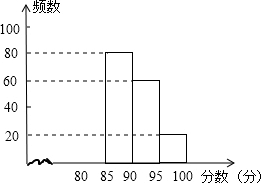
 某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:
某校组织了“安全在我心中”知识竞赛活动.根据获奖同学在竞赛中的成绩制成的统计图表如下:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | b |
| 90≤x<95 | 60 | c |
| 95≤x<100 | 20 | 0.1 |
分析 (1)首先用分数在95≤x<100之间的人数÷频率得到总人数,根据频率=$\frac{频数}{总数}$分别计算出a、b、c的值,补全统计图;
(2)用成绩在95分以上(含95分)的人数除以总人数即可;
(3)根据中位数的定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数,结合统计图可得答案,根据加权平均数公式计算可得平均分.
解答 解:(1)∵总人数为:20÷0.1=200(人),
∴a=200×0.2=40(人),
b=80÷200=0.4,
c=60÷200=0.3,
补全频数分布直方图如图: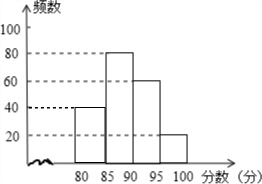
(2)可得获奖的同学获得特等奖的概率是$\frac{20}{200}$=0.1;
(3)把所用数据从小到大排列,位置处于中间的是第100名和101名,由统计图可以看出第100名和101名成绩落在85≤x<90分数段,
平均分为:$\frac{82.5×40+87.5×80+92.5×60+97.5×20}{200}$=89(分).
点评 此题主要考查了频数分布直方图,频数分布表,中位数,以及概率公式,读图时要全面细致,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.掌握好概率、中位数、加权平均数的概念.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
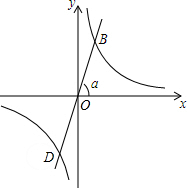 如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.
如图,正比例函数的图象与x轴正方向所成角为α度,若它与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B和点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2tan60° | B. | $\sqrt{8}$ | C. | $\root{3}{16}$ | D. | π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com