练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．计算：
    （1）$（2-π）^{0}+（\frac{1}{3}）^{-1}+（-2）^{3}$          
    （2）（2a-b-3）（2a+b-3）

    分析 （1）根据零指数幂和负整数指数幂计算即可；
    （2）根据完全平方公式计算即可．

    解答 解：（1）$（2-π）^{0}+（\frac{1}{3}）^{-1}+（-2）^{3}$=1+3-8=-4              
    （2）（2a-b-3）（2a+b-3）=（2a-3）2-b2=4a2-12ab+9-b2．

    点评 此题考查整式的混合计算，关键是根据整式的混合计算顺序解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）（$\frac{2}{3}$）-1+（π-3）0+（-2）-2+|（-2）3|
    （2）（9x3y-12xy3+3xy2）÷（-3xy）-（2y+x）（2y-x），其中x=1，y=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图所示，通过平移，△ABC的顶点A移到点D，画出平移后的图形，并找出图中所有平行且相等的线段．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

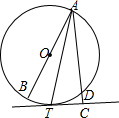    2．如图，AB是⊙O的直径，D是⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C
    （1）求证：CT为⊙O的切线；
    （2）若AD=2，TC=$\sqrt{3}$，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

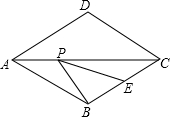    9．如图，菱形ABCD的边长为4，∠DAB=60°，E为BC的中点，在对角线AC上存在一点P，使△PBE的周长最小，则△PBE的周长的最小值为2$\sqrt{3}$+2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

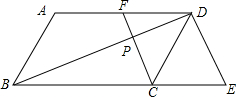    19．如图，在平行四边形ABCD中，F是AD的中点，延长BC到点E，使CE=$\frac{1}{2}$BC，连结DE、CF，连接BD交CF于点P．
    （1）求证：四边形CEDF是平行四边形；
    （2）若AB=4，AD=6，∠ABC=60°，求△DCE的周长；
    （3）在（2）的条件下，求△BPC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．计算：（$\frac{1}{a}+\frac{b}{a}$）$•\frac{2a}{b+1}$=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

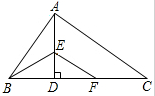    3．如用，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于E，EF∥AC，下列结论中：①AB=BF；②AE=ED；③AD=DC；④∠ABE=∠DFE；⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$，正确的是（　　）
    A．①③B．①⑤C．③④D．①②⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

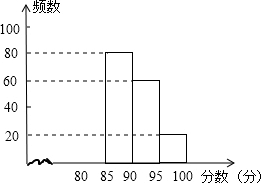    4．某校组织了“安全在我心中”知识竞赛活动．根据获奖同学在竞赛中的成绩制成的统计图表如下：
    分数段频数频率
    80≤x＜85a0.2
    85≤x＜9080b
    90≤x＜9560c
    95≤x＜100200.1
    根据以上图表提供的信息，解答下列问题：
    （1）求出表中a、b、c的数值，并补全频数分布直方图；
    （2）如果成绩在95分以上（含95分）的可以获得特等奖，那么获奖的同学获得特等奖的概率是多少？
    （3）获奖成绩的中位数落在哪个分数段？并估算全部获奖同学的平均分．

    查看答案和解析>>

    同步练习册答案