
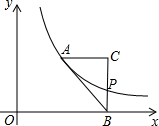
 已知Rt△ABC(∠C=90°)是一块形状与大小均会发生变化的三角形纸板,在平面直角坐标系中,将△ABC按如图放置,AC∥x轴,点B在x轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象经过点A,与线段BC相交于点P,且A,P两点的横坐标分别为a,2a+2.
已知Rt△ABC(∠C=90°)是一块形状与大小均会发生变化的三角形纸板,在平面直角坐标系中,将△ABC按如图放置,AC∥x轴,点B在x轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象经过点A,与线段BC相交于点P,且A,P两点的横坐标分别为a,2a+2.分析 (1)由反比例函数的解析式得出点A、P的坐标,求出BC、AC,由△ABC的面积得出方程,解方程即可求出a的值;
(2)若点P为BC中点,根据点A、P的坐标得出方程,方程无解,即可得出结论.
解答 解:(1)∵AC∥x轴,∠C=90°,
∴∠OBC=90°,
∵反比例函数y=$\frac{4}{x}$(x>0)的图象经过点A,与线段BC相交于点P,且A,P两点的横坐标分别为a,2a+2.
∴点A(a,$\frac{4}{a}$),P(2a+2,$\frac{2}{a+1}$),
∴BC=$\frac{4}{a}$,AC=2a+2-a=a+2,
∵△ABC的面积为6,
∴$\frac{1}{2}$×$\frac{4}{a}$×(a+2)=6,
解得:a=1;
(2)不存在;理由如下:
∵A(a,$\frac{4}{a}$),P(2a+2,$\frac{2}{a+1}$),
若点P为BC中点,则$\frac{4}{a}$=2×$\frac{2}{a+1}$,此方程无解,
∴不存在点P为BC中点的情况.
点评 本题是反比例函数综合题目,考查了坐标与图形特征、直角三角形面积的计算、反比例函数解析式的运用以及解方程等知识;本题综合性强,有一定难度,熟练掌握反比例函数图象上点的坐标特征是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 最高气温(℃) | 22 | 24 | 23 | 27 | 24 | 23 | 20 |
| A. | 22℃ | B. | 23℃ | C. | 24℃ | D. | 25℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).
如图,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对重庆市中学生每天学习所用时间的调查 | |
| B. | 对全国中学生心理健康现状的调查 | |
| C. | 对某班学生进行6月5日是“世界环境日”知晓情况的调查 | |
| D. | 对重庆市初中学生课外阅读量的调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com