
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x-y=2①}\\{2x+y=1②}\end{array}\right.$,
①+②得:3x=3,即x=1,
把x=1代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}x=1\\ y=-1\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x+y=8①}\\{4x-2y=5②}\end{array}\right.$,
①×2+②得:10x=21,即x=2.1,
把x=2.1代入①得:y=1.7,
则方程组的解为$\left\{\begin{array}{l}x=2.1\\ y=1.7\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:填空题
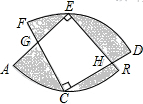 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且C是$\widehat{AB}$的中点,若扇形的半径为4,则图中四边形EGCH的面积为8平方单位.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且C是$\widehat{AB}$的中点,若扇形的半径为4,则图中四边形EGCH的面积为8平方单位.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| … | 第1列 | 第2列 | 第3列 | 第4列 |
| 第1行 | 1 | 4 | 5 | 10 |
| 第2行 | 4 | 8 | 10 | 12 |
| 第3行 | 9 | 12 | 15 | 14 |
| … | … | … | … | … |
| A. | 1次 | B. | 2次 | C. | 3次 | D. | 4次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
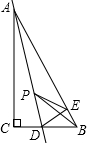 如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是4.
如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$a6b3 | B. | -$\frac{27}{8}$a6b3 | C. | $\frac{27}{8}$a6b3 | D. | -$\frac{27}{8}$a5b3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com