
分析 可将题目所给的可将题目所给的($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2=3($\sqrt{ab}$+$\sqrt{ac}$-$\sqrt{bc}$),进行适当变形,转换为几个完全平方式,然后根据非负数的性质求出a、b、c三边的数量关系,进而可判断出△ABC的形状.
解答 解:由($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2=3($\sqrt{ab}$+$\sqrt{ac}$-$\sqrt{bc}$),
得:a+b+c-$\sqrt{ab}$-$\sqrt{ac}$-$\sqrt{bc}$=0,
则($\sqrt{a}$-$\sqrt{b}$)2+($\sqrt{b}$-$\sqrt{c}$)2+($\sqrt{c}$-$\sqrt{a}$)2=0,
所以a=b=c,
∴△ABC是等边三角形.
点评 本题考查了配方法的应用,关键是对要求的式子进行变形和因式分解,将已知的等式转化为偶次方的和,根据非负数的性质解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
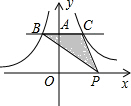 如图,反比例函数$y=-\frac{3}{x}$和$y=\frac{7}{x}$上分别有两点B、C,且BC∥x轴,点P是x轴上一动点,则△BCP的面积是5.
如图,反比例函数$y=-\frac{3}{x}$和$y=\frac{7}{x}$上分别有两点B、C,且BC∥x轴,点P是x轴上一动点,则△BCP的面积是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
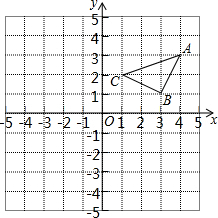 如图,将△ABC平移得到△A1B1C1,使A1点坐标为(1,1)
如图,将△ABC平移得到△A1B1C1,使A1点坐标为(1,1)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com