
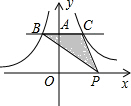
 如图,反比例函数$y=-\frac{3}{x}$和$y=\frac{7}{x}$上分别有两点B、C,且BC∥x轴,点P是x轴上一动点,则△BCP的面积是5.
如图,反比例函数$y=-\frac{3}{x}$和$y=\frac{7}{x}$上分别有两点B、C,且BC∥x轴,点P是x轴上一动点,则△BCP的面积是5. 分析 将△ABP的面积分为△ACP和△BCP两部分,根据反比例函数系数k的几何意义求得它们的面积,再相加即可求解.
解答 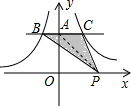 解:连结AC,
解:连结AC,
∵反比例函数$y=-\frac{3}{x}$和$y=\frac{7}{x}$上分别有两点B、C,BC∥x轴,
∴设B(-$\frac{3}{m}$,m),C($\frac{7}{m}$,m),
△BCP的面积=△ABP的面积+△ACP的面积
=$\frac{1}{2}$×$\frac{3}{m}$•m+$\frac{1}{2}$×$\frac{7}{m}$•m
=5.
故答案为:5.
点评 本题考查了反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.


科目:初中数学 来源: 题型:解答题
| 苹果种类 | 甲 | 乙 | 丙 |
| 每辆汽车装载量(吨) | 8 | 6 | 5 |
| 每吨苹果获利(百元) | 12 | 16 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
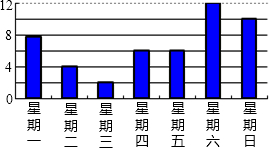 如图是明明作的一周的零用钱开支的统计图(单位:元)
如图是明明作的一周的零用钱开支的统计图(单位:元) 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com