
【题目】二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b﹣2c|,Q=|2a﹣b|﹣|3b+2c|,则P,Q的大小关系是 . 
【答案】P>Q
【解析】解:∵抛物线的开口向下,
∴a<0,
∵﹣ ![]() >0,
>0,
∴b>0,
∴2a﹣b<0,
∵﹣ ![]() =1,
=1,
∴b+2a=0,
x=﹣1时,y=a﹣b+c<0.
∴﹣ ![]() b﹣b+c<0,
b﹣b+c<0,
∴3b﹣2c>0,
∵抛物线与y轴的正半轴相交,
∴c>0,
∴3b+2c>0,
∴p=3b﹣2c,
Q=b﹣2a﹣3b﹣2c=﹣2a﹣2b﹣2c,
∴Q﹣P=﹣2a﹣2b﹣2c﹣3b+2c=﹣2a﹣5b=﹣4b<0
∴P>Q,
所以答案是:P>Q.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小),还要掌握二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c))的相关知识才是答题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 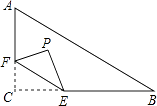
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国”.某区中小学每年都要举办一届科技比赛.如图为某区某校2015年参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图: 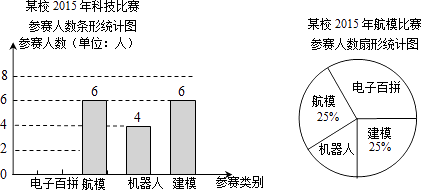
(1)该校参加机器人、建模比赛的人数分别是人和人;
(2)该校参加科技比赛的总人数是人,电子百拼所在扇形的圆心角的度数是°,并把条形统计图补充完整.
(3)从全区中小学参加科技比赛选手中随机抽取85人,其中有34人获奖.2015年某区中小学参加科技比赛人数共有3625人,请你估算2015年参加科技比赛的获奖人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点F在ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB. 
(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,sin∠CBE= ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正确的个数是( ) 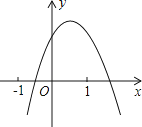
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx的图象过点A(﹣1,3),顶点B的横坐标为1.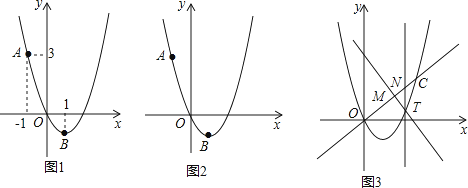
(1)求这个二次函数的表达式;
(2)点P在该二次函数的图象上,点Q在x轴上,若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)如图3,一次函数y=kx(k>0)的图象与该二次函数的图象交于O、C两点,点T为该二次函数图象上位于直线OC下方的动点,过点T作直线TM⊥OC,垂足为点M,且M在线段OC上(不与O、C重合),过点T作直线TN∥y轴交OC于点N.若在点T运动的过程中, ![]() 为常数,试确定k的值.
为常数,试确定k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数y=﹣ ![]() (x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y=
(x<0)的图象上,将此矩形向右平移3个单位长度到A1B1O1C1的位置,此时点A1在函数y= ![]() (x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
(x>0)的图象上,C1O1与此图象交于点P,则点P的纵坐标是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3,﹣1, ![]() ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组  无解,且使关于x的分式方程
无解,且使关于x的分式方程 ![]() ﹣
﹣ ![]() =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
A.﹣3
B.﹣2
C.﹣ ![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com