
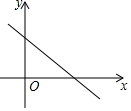
 如图,已知一次函数y=-x+4与反比例函数y=$\frac{k}{x}$(k为常数,k≠0).
如图,已知一次函数y=-x+4与反比例函数y=$\frac{k}{x}$(k为常数,k≠0).分析 (1)由$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{k}{x}}\end{array}\right.$,消去y得到,x2-4x+k=0,由题意△>0列出不等式即可解决问题.
(2)画出函数y=-x+4与y=$\frac{3}{x}$的图象,如图1所示,可知它们的交点坐标为A(1,3),B(3,1),x+$\frac{k}{x}$<4的解集,即$\frac{k}{x}$<-x+4的解集,由图象可知反比例函数图象在直线的下方部分对应的自变量的取值范围,即可解集.
(3)设E(x1,y1),F(x2,y2),由$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{k}{x}}\end{array}\right.$,消去y得到,x2-4x+k=0,推出x1+x2=4,x1x2=k,y1+y2=4,y1y2=k,(x1-x2)2=(y1-y2)2=16-4k,列出方程即可解决问题.
解答 解:(1)由$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{k}{x}}\end{array}\right.$,消去y得到,x2-4x+k=0,
由题意△>0,
∴16-4k>0,
∴k<4,
∴最大的整数k为3.
(2)画出函数y=-x+4与y=$\frac{3}{x}$的图象,如图1所示,可知它们的交点坐标为A(1,3),B(3,1),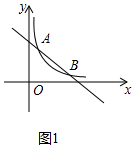
x+$\frac{k}{x}$<4的解集,即$\frac{k}{x}$<-x+4的解集,由图象可知$\frac{k}{x}$<-x+4的解集为1<x<3.
(3)设E(x1,y1),F(x2,y2),
由$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{k}{x}}\end{array}\right.$,消去y得到,x2-4x+k=0,
∴x1+x2=4,x1x2=k,y1+y2=4,y1y2=k,
∴(x1-x2)2=(y1-y2)2=16-4k,
∵EF=5$\sqrt{2}$,
∴(x1-x2)2+(y1-y2)2=50,
∴32-8k=50,
∴k=-$\frac{9}{4}$.
点评 本题考查反比例函数综合题、一次函数的应用、一元一次不等式、二元二次方程的根与系数的关系等知识,解题的关键是灵活运用所学知识,学会利用参数,构建方程解决问题,属于中考压轴题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
 在直角坐标系中,点C的坐标为(-3,0),将线段OC绕原点O顺时针旋转120°,得到线段OB.
在直角坐标系中,点C的坐标为(-3,0),将线段OC绕原点O顺时针旋转120°,得到线段OB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )
某校随机抽取了九年级的30名学生,测试了他们1分钟仰卧起坐的次数,并绘制如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在24.5~29.5之间的频率是( )| A. | 0.1 | B. | 0.17 | C. | 0.33 | D. | 0.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
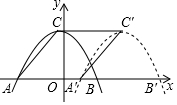 如图,抛物线的顶点为C(-1,8),交x轴于A(-7,0)与点B.将此抛物线向右平移使得A,B,C分别移至A',B',C',若四边形CAA'C'为菱形,则点B′的坐标为( )
如图,抛物线的顶点为C(-1,8),交x轴于A(-7,0)与点B.将此抛物线向右平移使得A,B,C分别移至A',B',C',若四边形CAA'C'为菱形,则点B′的坐标为( )| A. | (5,0) | B. | (13,0) | C. | (15,0) | D. | (17,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com