
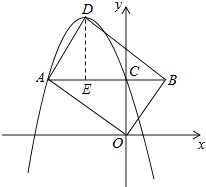
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C,过点C作CA∥x轴交抛物线于点A,在AC延长线上取点B,使BC= ![]() AC,连接OA,OB,BD和AD.
AC,连接OA,OB,BD和AD.
(1)若点A的坐标是(﹣4,4).
①求b,c的值;
②试判断四边形AOBD的形状,并说明理由;
(2)是否存在这样的点A,使得四边形AOBD是矩形?若存在,请直接写出一个符合条件的点A的坐标;若不存在,请说明理由.
【答案】
(1)
解:①∵AC∥x轴,A点坐标为(﹣4,4).
∴点C的坐标是(0,4)
把A、C两点的坐标代入y=﹣x2+bx+c得,
![]() ,
,
解得 ![]() ;
;
②四边形AOBD是平行四边形;
理由如下:
由①得抛物线的解析式为y=﹣x2﹣4x+4,
∴顶点D的坐标为(﹣2,8),
过D点作DE⊥AB于点E,
则DE=OC=4,AE=2,
∵AC=4,
∴BC= ![]() AC=2,
AC=2,
∴AE=BC.
∵AC∥x轴,
∴∠AED=∠BCO=90°,
∴△AED≌△BCO,
∴AD=BO.∠DAE=∠OBC,
∴AD∥BO,
∴四边形AOBD是平行四边形.
(2)
解:存在,点A的坐标可以是(﹣2 ![]() ,2)
,2)
要使四边形AOBD是矩形;
则需∠AOB=∠BCO=90°,
∵∠ABO=∠OBC,
∴△ABO∽△OBC,
∴ ![]() ,
,
又∵AB=AC+BC=3BC,
∴OB= ![]() BC,
BC,
∴在Rt△OBC中,根据勾股定理可得:OC= ![]() BC,AC=
BC,AC= ![]() OC,
OC,
∵C点是抛物线与y轴交点,
∴OC=c,
∴A点坐标为(﹣ ![]() c,c),
c,c),
∴顶点横坐标 ![]() =﹣
=﹣ ![]() c,b=﹣
c,b=﹣ ![]() c,
c,
顶点D纵坐标是点A纵坐标的2倍,为2c,
顶点D的坐标为(﹣ ![]() c,2c)
c,2c)
∵将D点代入可得2c=﹣(﹣ ![]() c)2+
c)2+ ![]() c
c ![]() c+c,
c+c,
解得:c=2或者0,
当c为0时四边形AOBD不是矩形,舍去,故c=2;
∴A点坐标为(﹣2 ![]() ,2).
,2).
【解析】(1)①将抛物线上的点的坐标代入抛物线即可求出b、c的值;
②求证AD=BO和AD∥BO即可判定四边形为平行四边形;(2)根据矩形的各角为90°可以求得△ABO∽△OBC即 ![]() ,再根据勾股定理可得OC=
,再根据勾股定理可得OC= ![]() BC,AC=
BC,AC= ![]() OC,可求得横坐标为﹣
OC,可求得横坐标为﹣ ![]() c,纵坐标为c.
c,纵坐标为c.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD 是一段斜坡,AB 是水平线,现为了测斜坡上一点 D 的铅直高度(即 垂线段 DB 的长度),小亮在点 D 处立上一竹竿 CD,并保证 CD=AB,CD⊥AD,然后在竿顶 C 处垂下一根细绳(细绳末端挂一重锤,以使细绳与水平线垂直),细绳与斜坡 AD 交于点E,此时他测得 CE=8 m,AE=6 m,求 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.
(1)求抛物线的函数表达式,并求出点D的坐标;
(2)如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(3)在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.
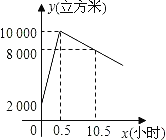
(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气;
(2)当x≥0.5时,求储气罐中的储气量y(立方米)与时间x(小时)的函数解析式;
(3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,小球在带你B位置时达到最低点,当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°.(取sin37°=0.6,cos37°=0.8,tan37°=0.75) 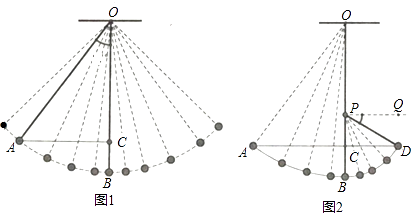
(1)求点A与点B的高度差BC的值.
(2)如图2,若在点O的正下方有一个阻碍物P,当小球从左往右落到最低处后,运动轨迹改变,变为以P为圆心,PB为半径继续向右摆动,当摆动至与点A在同一水平高度的点D时,满足PD部分细绳与水平线的夹角∠DPQ=30°,求OP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为_________.(π取3)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com