
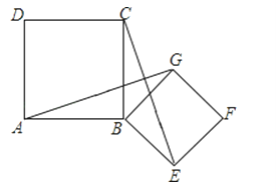
【题目】如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由ABCD、BEFG均为正方形,得出AB=CB,∠ABC=∠GBE=90°,BG=BE,得出∠ABG=∠CBE,从而得到△ABG≌△CBE,即可得到结论;
(2)由△ABG≌△CBE,得出∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.
试题解析:(1)∵四边形ABCD、BEFG均为正方形,∴AB=CB,∠ABC=∠GBE=90°,BG=BE,∴∠ABG=∠CBE,在△ABG和△CBE中,∵AB=CB,∠ABG=∠CBE,BG=BE,∴△ABG≌△CBE(SAS),∴AG=CE;
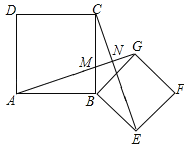
(2)如图所示:∵△ABG≌△CBE,∴∠BAG=∠BCE,∵∠ABC=90°,∴∠BAG+∠AMB=90°,∵∠AMB=∠CMN,∴∠BCE+∠CMN=90°,∴∠CNM=90°,∴AG⊥CE.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为8,⊙O经过点C和点D,且与AB相切于点E.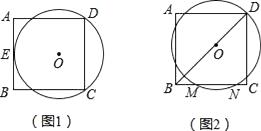
(1)求⊙O的半径;
(2)如图2,平移⊙O,使点O落在BD上,⊙O经过点D,BC与⊙O交于M,N,求MN2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
(1)找出图中相等的锐角,并说明理由.
(2)求出点![]() 到直线
到直线![]() 的距离以及点
的距离以及点![]() 到直线
到直线![]() 的距离.
的距离.
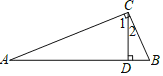
解:(1)![]() (已知),
(已知),
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() .
.
同理可证,
![]() .
.
(2)点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() .
.
![]() 到直线
到直线![]() 的距离为线段 的长度.
的距离为线段 的长度.
![]()
![]()
![]()
![]() (填线段名称).
(填线段名称).
![]() ,
,![]() ,
,![]() ,代入上式,解得
,代入上式,解得
![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在网格中画对称图形.
(1)如图是五个小正方形拼成的图形,请你移动其中一个小正方形,重新拼成一个图形,使得所拼成的图形满足下列条件,并分别画在图①、图②、图③中(只需各画一个,内部涂上阴影);
①是轴对称图形,但不是中心对称图形;
②是中心对称图形,但不是轴对称图形;
③既是轴对称图形,又是中心对称图形.
(2)请你在图④的网格内设计一个商标,满足下列要求:
①是顶点在格点的凸多边形(不是平行四边形);
②是中心对称图形,但不是轴对称图形;
③商标内部涂上阴影.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:在综合实践课上,老师让同学们在已知三角形的基础上,经过画图,探究三角形边之间存在的关系.如图,已知点![]() 在
在![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 且
且![]() ,在
,在![]() 上截取
上截取![]() ,再作
,再作![]() 交线段
交线段![]() 于点
于点![]() .
.

实践操作
(1)尺规作图:作出符合上述条件的图形;
探究发现
(2)勤奋小组在作出图形后,发现![]() ,
,![]() ,请说明理由;
,请说明理由;
探究应用
(3)缜密小组在勤奋小组探究的基础上,测得![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为人. 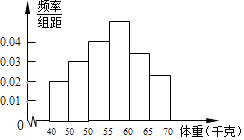
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE= ![]() AB;③S△ADE=
AB;③S△ADE= ![]() S△ABC . 正确的有( )
S△ABC . 正确的有( )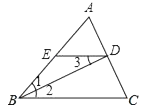
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com