
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线, 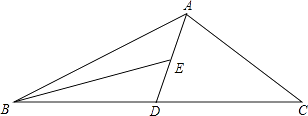
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
【答案】
(1)解:∵∠BED是△ABE的一个外角,
∴∠BED=∠ABE+∠BAD=15°+35°=50°
(2)解:如图所示,EF即是△BED中BD边上的高
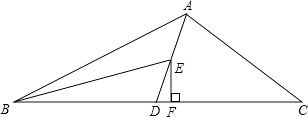
(3)解:∵AD为△ABC的中线,BE为三角形ABD中线,
∴S△BED= ![]() S△ABC=
S△ABC= ![]() ×60=15;
×60=15;
∵BD=5,
∴EF=2S△BED÷BD=2×15÷5=6,
即点E到BC边的距离为6
【解析】(1)利用三角形的外角等于与它不相邻的两个内角之和即可求∠BED的度数;(2)△BED是钝角三角形,所以BD边上的高在BD的延长线上;(3)先根据三角形的中线把三角形分成面积相等的两个小三角形,结合题意可求得△BED的面积,再直接求点E到BC边的距离即可.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE. 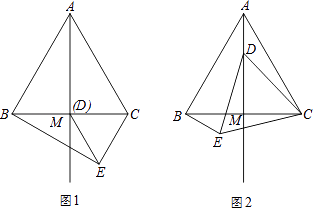
(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
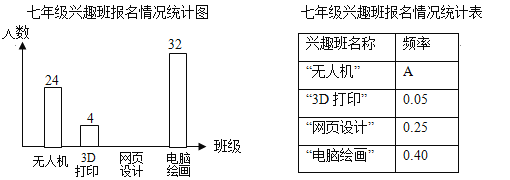
【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,请回答下列问题:
(1)报名参加兴趣班的总人数为 人;统计表中的A= ;
(2)将统计图补充完整;
(3)为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
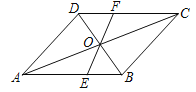
【题目】如图所示,在□ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
(1)求证:OE=OF;
(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线. 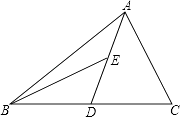
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为40,BD=5,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择.其中甲型机器每日生产零件106个,乙型机器每日生产零件60个,经调査,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元
(1)求甲、乙两种机器每台各多少万元?
(2)如果工厂期买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
(3)在(2)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金.应该选择哪种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com