
【题目】如图,已知△ABC,AB=AC,AD是△ABC的角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,M,F.若∠CAD=20°,求∠MCD的度数.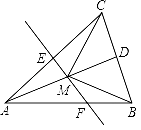
【答案】解:∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∵∠CAD=20°,
∴∠ACD=70°,
∵EF垂直平分AC,
∴AM=CM,
∴∠ACM=∠CAD=20°,
∴∠MCD=50°
【解析】根据等腰三角形的性质得到AD⊥BC,根据三角形的内角和得到∠ACD=70°,根据线段垂直平分线的性质得到∠ACM=∠CAD=20°,于是得到结论.
【考点精析】通过灵活运用三角形的内角和外角和线段垂直平分线的性质,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知甲、乙、丙三个旅游团的游客人数都相等,且每个团游客的平均年龄都是30岁,这三个团游客年龄的方差分别是S甲2=1.4,S乙2=18.8.S丙2=25,导游小芳喜欢带游客年龄相近的团队,若要在这三个团中选择一个,则她应选( )
A.甲
B.乙
C.丙
D.哪一个都可以
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中, 
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标.
(3)求出三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
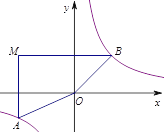
【题目】如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=![]() 的图象交于A、B两点,则四边形MAOB的面积为________.
的图象交于A、B两点,则四边形MAOB的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于( ) 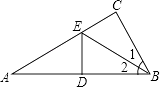
A.3cm
B.4cm
C.6cm
D.9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,BD是△ABC的中线,∠ADB=120°,点E在中线BD的延长线上,则△ACE是直角三角形时,DE的长为 . 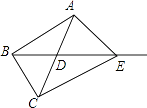
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,下列说法中错误的是( ) 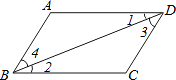
A.∵∠A+∠ADC=180°,∴AB∥CD
B.∵AB∥CD,∴∠ABC+∠C=180°
C.∵∠1=∠2,∴AD∥BC
D.∵AD∥BC,∴∠3=∠4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com