
【题目】如图,在△ABC中,AB=AC=4,BD是△ABC的中线,∠ADB=120°,点E在中线BD的延长线上,则△ACE是直角三角形时,DE的长为 . 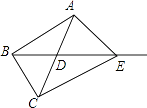
【答案】2或4
【解析】解:△ACE为直角三角形分三种情况: ①当∠CAE=90°时,
∵∠ADB=120°,
∴∠ADE=60°,∠AED=30°.
∵AB=AC=4,BD是△ABC的中线,
∴AD=CD=2.
∴DE= ![]() =
= ![]() =4;
=4;
②当∠AEC=90°时,
∵ED是△EAC的中线,
∴DE= ![]() AC=2;
AC=2;
③当∠ACE=90°时,
∵∠ADB=120°,
∴∠CDE=60°,∠CED=30°.
∵AB=AC=4,BD是△ABC的中线,
∴AD=CD=2.
∴DE= ![]() =
= ![]() =4.
=4.
综上可知:DE的长为2或4.
所以答案是:2或4.
【考点精析】利用等腰三角形的性质和含30度角的直角三角形对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.


科目:初中数学 来源: 题型:
【题目】据国家统计局数据,2018年全年国内生产总值为90.3万亿,比2017年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份是( )
A. 2019年B. 2020年C. 2021年D. 2022年
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AB=AC,AD是△ABC的角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,M,F.若∠CAD=20°,求∠MCD的度数.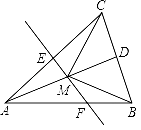
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双营服装店老板到厂家选购A、B两种型号的服装,若购进A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元,
(1)求A,B两种型号的服装每件分别多少元?
(2)若销售1件A型服装可获利18元,销售1件B型服装可获利30元,根据市场需求,服装店老板决定,购进A型服装的数量要比购进B型服装数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后,可使总的获利不少于699元,问有几种进货方案如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地以每千克a元的价格购进一种水果m千克,运输过程中重量损失了10%,超市在进价的基础上増加了30%作为售价,假定不计超市其他费用,那么售完这种水果,超市获得的利润是_____元(用含m、a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.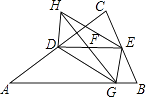
(1)求证:四边形HDGE是平行四边形.
(2)已知∠C=90°,∠A=30°,AB=4.
①当AG为何值时,四边形HDGE是矩形;
②当AG为何值时,四边形HDGE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( ) 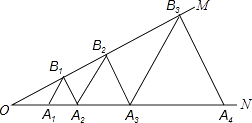
A.6
B.12
C.32
D.64
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com