
【题目】如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.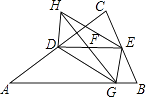
(1)求证:四边形HDGE是平行四边形.
(2)已知∠C=90°,∠A=30°,AB=4.
①当AG为何值时,四边形HDGE是矩形;
②当AG为何值时,四边形HDGE是菱形.
【答案】
(1)
证明:∵HF=GF,DF=EF,
∴四边形HDGE是平行四边形
(2)
解:∵∠C=90°,∠A=30°,AB=4,
∴AC=ABcom∠A=4× ![]() =2
=2 ![]() ,BC=4×
,BC=4× ![]() =2,∠B=60°,
=2,∠B=60°,
∵AC的中点为D,BC的中点为E,F是DE的中点,
∴BE=1,DE= ![]() AB=2,AD=CD=
AB=2,AD=CD= ![]() ,DF=EF=1,DE∥AB,
,DF=EF=1,DE∥AB,
∴∠CBD=∠B=60°,
① 当AG=3或2时,四边形HDGE是矩形,
当AG=3时,如图1,
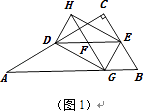
BG=4﹣3=1,
∴BG=CE,
BG=BE=EG=1=CE,DE=DE,∠CED=∠DEG=60°,
在△DGE和△DCE中,  ,
,
∴△DGE≌△DCE,
∴∠DGE=∠DCE=90°,
∴四边形HDGE是矩形;
当AG=2时,则AG=BG,
∴DG∥CE,EG∥AC,H,C重合,
∴∠DCE=90°,∴四边形HDGE是矩形,如图2;
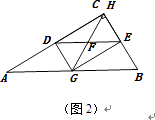
②过F作MN⊥DE,交AC于M,AB与N,
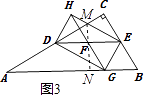
∵DE∥AB,
∴MN⊥AB,∠MDF=∠A=30°,
∵F是DE的中点,
∴MN是线段DE的垂直平分线,
∴ND=NE,
∵DF=1,MB= ![]() ,
,
∵AD= ![]() ,
,
∴AM= ![]() ,
,
∴AN=AMcom∠A= ![]()
![]() =
= ![]() ,
,
当AG=AN= ![]() 时,G在DE的中垂线上,DG=GE,四边形HDGE是菱形.
时,G在DE的中垂线上,DG=GE,四边形HDGE是菱形.
【解析】(1)由平行四边形的判定直接推出;(2)根据直角三角形的性质得到AB=4,求得AC=2 ![]() ,BC=4×
,BC=4× ![]() =2,∠B=60°,根据三角形的中位线得到BE=1,DE=2,AD=
=2,∠B=60°,根据三角形的中位线得到BE=1,DE=2,AD= ![]() ,DF=EF=1,根据平行线的性质得到∠CBD=∠B=60°,①当AG=3或2时,四边形HDGE是矩形.当AG=3时,根据全等三角形的性质得到∠DGE=∠DCE=90°,于是得到四边形HDGE是矩形;当AG=2时,则AG=BG,推出∠DCE=90°,于是得到四边形HDGE是矩形;②过F作MN⊥DE,交AC于M,AB与N,根据全等三角形的性质得到∠MDF=∠A=30°根据线段垂直平分线的性质得到ND=NE,求得AN=AMcom∠A=
,DF=EF=1,根据平行线的性质得到∠CBD=∠B=60°,①当AG=3或2时,四边形HDGE是矩形.当AG=3时,根据全等三角形的性质得到∠DGE=∠DCE=90°,于是得到四边形HDGE是矩形;当AG=2时,则AG=BG,推出∠DCE=90°,于是得到四边形HDGE是矩形;②过F作MN⊥DE,交AC于M,AB与N,根据全等三角形的性质得到∠MDF=∠A=30°根据线段垂直平分线的性质得到ND=NE,求得AN=AMcom∠A= ![]() ,当AG=AN=
,当AG=AN= ![]() 时,G在DE的中垂线上,根据菱形的判定即可得到结论.
时,G在DE的中垂线上,根据菱形的判定即可得到结论.
【考点精析】本题主要考查了两点间的距离的相关知识点,需要掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,BD是△ABC的中线,∠ADB=120°,点E在中线BD的延长线上,则△ACE是直角三角形时,DE的长为 . 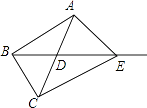
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A
相交于A![]() 和B(4,n),点P是直线AB上不同于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.设P点的横坐标为m.
和B(4,n),点P是直线AB上不同于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.设P点的横坐标为m.
(1)直接写出点B坐标;
(2)求抛物线的解析式;
(3)请用含m的代数式表示线段PC的长;
(4)若点P在线段AB上移动,请直接写出△PAC为直角三角形时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,下列说法中错误的是( ) 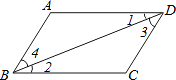
A.∵∠A+∠ADC=180°,∴AB∥CD
B.∵AB∥CD,∴∠ABC+∠C=180°
C.∵∠1=∠2,∴AD∥BC
D.∵AD∥BC,∴∠3=∠4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
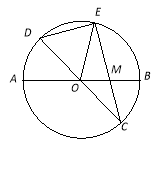
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=![]() .
.
(1)求证:![]() ;
;
(2)求EM的长;
(3)求sin∠EOB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com