
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A
相交于A![]() 和B(4,n),点P是直线AB上不同于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.设P点的横坐标为m.
和B(4,n),点P是直线AB上不同于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.设P点的横坐标为m.
(1)直接写出点B坐标;
(2)求抛物线的解析式;
(3)请用含m的代数式表示线段PC的长;
(4)若点P在线段AB上移动,请直接写出△PAC为直角三角形时点P的坐标.

【答案】(1)B(4,6),(2)抛物线的解析式为y=2x2﹣8x+6.(3)PC==2m2—9m+4;(4)点P的坐标为(3,5)或![]()
【解析】试题分析:(1)把点B(4,n)代入直线![]() 中即可求出n的值;(2)把点A、B的坐标代入抛物线
中即可求出n的值;(2)把点A、B的坐标代入抛物线![]() 中,得到一个关于a、b的二元一次方程组,解方程组即可,再写出抛物线的解析式;(3)设P点的横坐标为m,则点P的坐标为(m,m+2),点C的坐标为(m,2m2﹣8m+6);抛物线
中,得到一个关于a、b的二元一次方程组,解方程组即可,再写出抛物线的解析式;(3)设P点的横坐标为m,则点P的坐标为(m,m+2),点C的坐标为(m,2m2﹣8m+6);抛物线![]() 与x轴交点坐标为(4,0)和(
与x轴交点坐标为(4,0)和(![]() ,0),分两种情况求PC的长度:当点C在x轴上方时,即当
,0),分两种情况求PC的长度:当点C在x轴上方时,即当![]() <
<![]() 或
或![]() >4时,PC=(m+2)﹣(2m2﹣8m+6),化简即可;当点C在x轴下方时,即
>4时,PC=(m+2)﹣(2m2﹣8m+6),化简即可;当点C在x轴下方时,即![]() <
<![]() <4时,PC=(m+2)﹣(2m2﹣8m+6),化简即可;(3)图画即可写出;
<4时,PC=(m+2)﹣(2m2﹣8m+6),化简即可;(3)图画即可写出;
试题解析:
(1)B(4,6), (1分)
(2)∵A(![]() ,
,![]() )、B(4,6)在抛物线y=ax2+bx+6上,
)、B(4,6)在抛物线y=ax2+bx+6上,
∴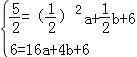 (3分)
(3分)
解得![]()
∴抛物线的解析式为y=2x2﹣8x+6. (4分)
(3)设动点P的坐标为(m,m+2),则C点的坐标为(m,2m2﹣8m+6),
当![]() <
<![]() <4时, (5分)
<4时, (5分)
PC=(m+2)﹣(2m2﹣8m+6),
=﹣2m2+9m﹣4 (6分)
当![]() <
<![]() 或
或![]() >4时, (7分)
>4时, (7分)
PC=(2m2﹣8m+6)—(m+2)
=2m2—9m+4 (8分)
(4)点P的坐标为(3,5)或![]() (10分)
(10分)


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
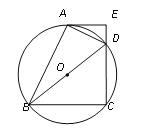
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双营服装店老板到厂家选购A、B两种型号的服装,若购进A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元,
(1)求A,B两种型号的服装每件分别多少元?
(2)若销售1件A型服装可获利18元,销售1件B型服装可获利30元,根据市场需求,服装店老板决定,购进A型服装的数量要比购进B型服装数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后,可使总的获利不少于699元,问有几种进货方案如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC的中点为D,BC的中点为E,F是DE的中点,动点G在边AB上,连接GF,延长GF到点H,使HF=GF,连接HD,HE.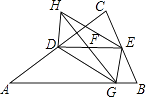
(1)求证:四边形HDGE是平行四边形.
(2)已知∠C=90°,∠A=30°,AB=4.
①当AG为何值时,四边形HDGE是矩形;
②当AG为何值时,四边形HDGE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,E,F分别是BC、AD的中点,连接AE、CF. 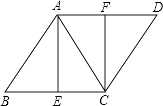
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨千米),铁路运价为1.2元/(吨千米),这两次运输共支出公路运费15 000元,铁路运费97200元. 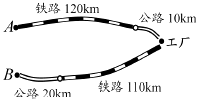
(1)求化工厂从A地购买这批原料及利用这批原料生产的产品各多少吨?
(2)计算这批产品的销售款比原料费和运输费的和多多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com