Question

【题目】完成下列证明过程，求证：三角形的中位线平行于三角形的第三边，并且等于第三边的一半．
已知：________
求证：________

Answer 1

【答案】在△ABC中，AD=DB，AE=EC|DE∥BC，DE= BC
证明：延长ED到点F，使DF=DE，连接FA、FB、BE．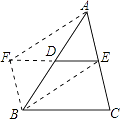

证明：延长ED到点F，使DF=DE，连接FA、FB、BE．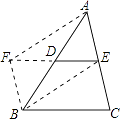

∵AD=BD，DE=DF
∴四边形AEBF是平行四边形．
∴BF∥AE，BF=AE，DE= EF，
∵AE=EC，∴BF∥CE，BF=CE，
∴四边形BCEF是平行四边形．
∴DE∥BC，EF=BC，
∴DE= EF= BC．
【解析】解：已知：在△ABC中，AD=DB，AE=EC，求证：DE∥BC，DE= BC．所以答案是：在△ABC中，AD=DB，AE=EC；DE∥BC，DE= BC．
根据文字题目证明要求写出已知、求证即可．先证明四边形AEBF是平行四边形，再证明四边形BCEF是平行四边形即可．
【考点精析】关于本题考查的三角形中位线定理，需要了解连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能得出正确答案．