
【题目】如图,在![]() △
△![]() 中,
中,![]() ,
,![]() 为斜边
为斜边![]() 上的中点,连接
上的中点,连接![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,分别与
,分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() .过点
.过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
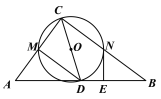
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),DP=1,AD=2,∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.

(1)求线段PC之长;
(2)求线段PN之长;
(3)如图2,连接AC,分别交PM,PB于点E,F.求线段EF之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)如图1,在△ABC中,点D,E,Q分别在AB,AC,BC上,且DE∥BC,AQ交DE于点P.求证:![]() .
.
(2)如图,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证MN2=DM·EN.
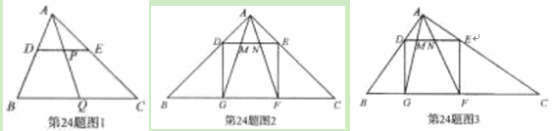
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随若移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A .和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如下图表(部分信息未给出):

根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(3)若该中学约有![]() 名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
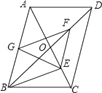
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
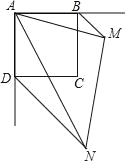
【题目】已知:如图,正方形ABCD,BM、DN分别是正方形的两个外角平分线,∠MAN=45°,将∠MAN绕着正方形的顶点A旋转,边AM、AN分别交两条角平分线于点M、N,联结MN.
(1)求证:△ABM∽△NDA;
(2)联结BD,当∠BAM的度数为多少时,四边形BMND为矩形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() ,直线l是它的对称轴,把该抛物线沿着x轴水平向左平移
,直线l是它的对称轴,把该抛物线沿着x轴水平向左平移![]() 个单位长度后,与x轴交于点A、B,
个单位长度后,与x轴交于点A、B,![]() 在B的左侧
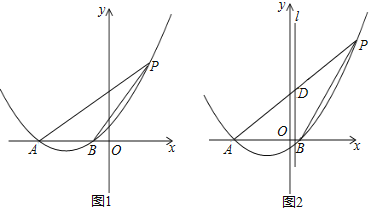
在B的左侧![]() ,如图1,P为平移后的抛物线上位于第一象限内的一点
,如图1,P为平移后的抛物线上位于第一象限内的一点
![]() 点A的坐标为______;
点A的坐标为______;
![]() 若点P的横坐标为
若点P的横坐标为![]() ,求出当m为何值时
,求出当m为何值时![]() 的面积最大,并求出这个最大值;
的面积最大,并求出这个最大值;
![]() 如图2,AP交l于点D,当D为AP的中点时,求证:
如图2,AP交l于点D,当D为AP的中点时,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com